수학방

로그함수 y = log_ax(a > 0, a ≠ 1)는 a > 1이면 증가함수, 0 < a < 1이면 감소함수예요. 정의역이 양의 실수 전체의 집합이면 최솟값은 0에 한없이 가까워지고, 최댓값은 그 끝을 알 수 없어요.

따라서 최대, 최소를 구한다는 건 정의역이 제한된 범위를 갖는다는 뜻이에요.

지수함수의 최대, 최소와 마찬가지로 양쪽 경계에서 최댓값 또는 최솟값을 갖죠.

a > 1일 때는 로그함수가 증가함수라서 x가 증가하면 y도 증가하므로 양쪽 경계 중 작은 값에서 최솟값, 큰 값에서 최댓값을 가져요.

0 < a < 1일 때는 로그함수가 감소함수라서 x가 증가하면 y는 감소하므로 양쪽 경계 중 작은 값에서 최댓값, 큰 값에서 최솟값을 가져요.

정의역이 {x|m ≤ x ≤ n}일 때, y = log_ax(a > 0, a ≠ 1)은

• a > 1일 때, x = m에서 최솟값 y = log_am, x = n일 때 최댓값 y = log_an
• 0 < a < 1일 때, x = m에서 최댓값 y = log_am, x = n일 때 최솟값 y = log_an

다음 함수의 최댓값과 최솟값을 구하여라.
(1) y = log₃(x + 4) - 2       (-3 ≥ x ≥ 5)
(2) y = log${}_{\frac{1}{2}}$(x - 2) + 1       (4 ≥ x ≥ 10)

(1) 밑이 3으로 1보다 크니까 증가함수예요. 경계 중 작은 값에서 최솟값을 갖고, 큰 값에서 최댓값을 가져요.

y = log₃(x + 4) - 2

x = -3일 때, 최솟값
log₃(-3 + 4) - 2
= log₃1 – 2
= 0 – 2
= -2

x = 5일 때, 최댓값
log₃(5 + 4) - 2
= log₃9 – 2
= log₃3² – 2
= 2 – 2
= 0

(2) 밑이 $\frac{1}{2}$로 0보다 크고 1보다 작으니까 감소함수예요. 경계 중 작은 값에서 최댓값을 갖고, 큰 값에서 최솟값을 가져요.

y = log${}_{\frac{1}{2}}$(x - 2) + 1

x = 10일 때, 최솟값
log${}_{\frac{1}{2}}$(10 - 2) + 1
= log${}_{\frac{1}{2}}$8 + 1
= log${}_{2^{-1}}$2³ + 1
= -3 + 1
= -2

로그함수를 이용해서 수의 대소를 비교할 수 있어요.

로그함수 y = log_ax(a > 0, a ≠ 1)는 다음과 같은 성질이 있어요.

• a > 1일 때 증가함수. x가 증가하면 y도 증가. x₁ < x₂이면, y₁ < y₂
• 0 < a < 1일 때 감소함수. x가 증가하면 y는 감소. x₁ < x₂이면, y₁ > y₂

그래프를 생각하면 쉬워요.

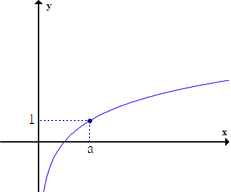
a > 1일 때, 진수 x가 크면 함숫값 y도 커요.

0 < a < 1일 때, 진수 x가 크면 함숫값 y는 작아요.

대소를 비교할 두 수를 밑이 같은 로그 꼴로 나타내요. 그 다음 밑이 1보다 큰지 작은지를 보고, 진수의 크기를 비교해서 두 수 중 어느 수가 더 큰지를 알 수 있어요.

다음 두 수의 대소를 비교하여라.
(1) 4, log₂8         (2) log${}_{\frac{1}{2}}$5, 3log${}_{\frac{1}{2}}\sqrt{3}$

(1)

4 → 4log₂2 = log₂2⁴ = log₂16

log₂8

진수를 비교해보죠. 16 > 8로 16이 더 커요.

밑이 2로 1보다 크니까 x가 증가하면 y도 증가해요. a > 1일 때, x₁ < x₂이면, y₁ < y₂

진수가 크면 수가 더 크니까 4 > log₂8이에요.

(2)

log${}_{\frac{1}{2}}$5

3log${}_{\frac{1}{2}}\sqrt{3}$ = log${}_{\frac{1}{2}}\sqrt{3}^{3}$

진수를 비교해보죠. 5 > $\sqrt{3}^{3}$으로 $\sqrt{3}^{3}$이 더 커요.

밑이 $\frac{1}{2}$로 1보다 작으니까 x가 증가하면 y는 감소해요. 0 < a < 1일 때, x₁ < x₂이면, y₁ > y₂

진수가 크면 수가 더 작으니까 log${}_{\frac{1}{2}}$5 > 3log${}_{\frac{1}{2}}\sqrt{3}$이에요.

지수함수 y = a^x(a > 0, a ≠ 1)는 a > 1이면 증가함수, 0 < a < 1이면 감소함수예요. 정의역이 실수 전체의 집합이면 최솟값은 0에 한없이 가까워지고, 최댓값은 그 끝을 알 수 없어요.

따라서 최대, 최소를 구한다는 건 정의역이 제한된 범위를 갖는다는 뜻이에요.

제한된 범위에서 함수의 최대, 최소를 구하는 건 1학년 때, 이차함수의 최댓값과 최솟값, 이차함수의 최대최소에서 해본 적이 있죠? 양쪽 경계나 꼭짓점에서 최댓값 또는 최솟값을 가져요.

지수함수는 꼭짓점이 없으니 양쪽 경계에서 최댓값 또는 최솟값을 갖죠.

지수함수와 지수함수의 그래프를 이용해서 수의 대소를 비교할 수 있어요.

지수함수 y = ax(a > 0, a ≠ 1)는 다음과 같은 성질이 있어요.

• a > 1일 때 증가함수. x가 증가하면 y도 증가. x₁ < x₂이면, y₁ < y₂
• 0 < a < 1일 때 감소함수. x가 증가하면 y는 감소. x₁ < x₂이면, y₁ > y₂

그래프를 생각하면 쉬워요.

a > 1일 때, 지수 x가 크면 함숫값 y도 커요.

0 < a < 1일 때, 지수 x가 크면 함숫값 y는 작아요.

대소를 비교할 두 수를 밑이 같은 지수 꼴로 나타내요. 그 다음 밑이 1보다 큰지 작은지를 보고, 지수의 크기를 비교해서 두 수 중 어느 수가 더 큰지를 알 수 있어요.

다음 두 수의 대소를 비교하여라.
(1) 2⁴, $8^{\frac{6}{5}}$
(2) $\left(\frac{1}{3}\right)^{2}$, $\left(\frac{1}{27}\right)^{\frac{8}{9}}$

(1)

2⁴

지수를 비교해보죠. 4 > $\frac{18}{5}$로 4가 더 커요

밑이 2로 1보다 크니까 x가 증가하면 y도 증가해요. a > 1일 때, x₁ < x₂이면, y₁ < y₂

지수가 크면 수가 더 크니까 2⁴ > $8^{\frac{6}{5}}$이에요.

(2)

지수를 비교해보죠. 2 < $\frac{8}{3}$로 $\frac{8}{3}$이 더 커요.

밑이 로 1보다 작으니까 x가 증가하면 y는 감소해요. 0 < a < 1일 때, x₁ < x₂이면, y₁ > y₂

지수가 크면 수가 더 작으니까 $\left(\frac{1}{3}\right)^{2}$ > $\left(\frac{1}{27}\right)^{\frac{8}{9}}$ 이에요.

수열의 귀납적 정의는 첫째 항과 "앞의 항 → 다음 항"의 관계를 알려줘요. a₁을 알면 a₂를 구할 수 있고, a₂를 알면 a₃를 구할 수 있어요.

"첫 단추를 잘 못 끼우다." 이런 표현 있죠? 처음 시작이 잘 못 되어 그 뒤로도 계속 잘못된 상태가 된다는 뜻이잖아요. 반대로 생각해서 첫 단추를 잘 끼우면 두 번째 단추도 잘 끼울 수 있고, 두 번째 단추를 잘 끼우면 세 번째 단추도 잘 끼울 수 있어요.

수학적 귀납법은 이와 비슷해요. "앞 단계 → 다음 단계"로 이어지는 구조를 이용해서 명제가 참임을 증명해요.

첫 번째일 때 명제가 성립해요. 그리고 어떤 하나가 성립하면 연속된 그 다음도 성립한다고 해보죠.

첫 번째가 성립하면 그 다음인 두 번째도 성립하겠죠? 두 번째가 성립하니까 그 다음인 세 번째도 성립해요. 세 번째가 성립하니까 그 다음인 네 번째도 성립하고, … 이렇게 계속하면 결국 모두 다 성립하는 걸 알 수 있어요.

수학적 귀납법으로 어떤 명제가 모든 자연수에서 성립함을 보이려면 딱 두 단계만 거치면 돼요.

수학적 귀납법
1. 기초 단계: n = 1일 때 성립 확인
2. 귀납 단계: n = k일 때 성립한다고 가정하고, n = k + 1에서도 성립함을 증명

이 두 단계를 거치면, 모든 자연수에 대해 참이라는 결론을 얻을 수 있어요.

다음 수열을 보죠.

a₁ = 1, a_{n + 1} = a_n + 2

첫째항이 1이고 공차가 2인 등차수열로 일반항이 a_n = 2n - 1이에요.

수열의 일반항이 a_n = 2n - 1이 맞는지 수학적 귀납법으로 증명해 볼까요?

1. 기초 단계: n = 1일 때

a_n = 2n - 1
    = 2 × 1 - 1 (∵ n = 1 대입)
    = 1
    = a₁

n = 1일 때, 식이 성립해요.

2. 귀납 단계: 어떤 자연수 k에 대하여 n = k일 때 a_k = 2k - 1성립하면, n = k + 1일 때도 식이 성립하는지 알아보죠.

a_k = 2k - 1
a_k + 2 = 2k - 1 + 2       (∵ 양변 + 공차 2)
a_{k + 1} = 2k + 1         (∵ a_{n + 1} = a_n + 2)
a_{k + 1} = 2(k + 1) - 1

a_n = 2n - 1에 n = k + 1을 대입한 것과 같으므로 n = k + 1일 때도 a_n = 2n - 1이 성립해요.

n = 1일 때, a_n = 2n - 1이 성립해요.
n = 1일 때 성립하니까 n = 2일 때도 성립해요.
n = 2일 때 성립하니까 n = 3일 때도 성립해요.
n = 3일 때 성립하니까 n = 4일 때도 성립해요.
…

따라서 모든 자연수 n에 대하여 a_n = 2n - 1이 성립함을 알 수 있어요.

모든 자연수 n에 대하여 다음 등식이 성립함을 수학적 귀납법을 이용하여 증명하여라.
(1) 1 + 2 + 3 + 4 + … + n = $\frac{n(1+n)}{2}$
(2) 1² + 2² + 3² + 4² + … + n² = $\frac{n(n+1)(2n+1)}{6}$

등차수열의 합과 여러 가지 수열의 합에서 봤던 공식이에요.

(1)

1. n = 1일 때, 등식이 성립하는지 확인해보죠.

(좌변) = 1

(우변) = $\frac{1(1+n)}{2}$ = $\frac{1(1 + 1)}{2}$ = 1

(좌변) = (우변)이므로 n = 1일 때 등식이 성립해요.

2. n = k일 때 등식이 성립하면 n = k + 1일 때도 성립하는지 확인해보죠.

1 + 2 + 3 + 4 + … + k
    = $\frac{k(1+k)}{2}$
1 + 2 + 3 + 4 + … + k + (k + 1)
    = $\frac{k(1+k)}{2}$ + (k + 1)         (∵ 양변 + (k + 1))
1 + 2 + 3 + 4 + … + k + (k + 1)
    = $\frac{1}{2}$(k + 1)(k + 2)
1 + 2 + 3 + 4 + … + k + (k + 1)
    = $\frac{1}{2}$(k + 1){1 + (k + 1)}

n = k + 1을 등식에 대입한 것과 같으므로 n = k + 1일 때도 등식이 성립해요.

따라서 이 등식은 모든 자연수 n에 대하여 성립해요.

(2)

1. n = 1일 때, 등식이 성립하는지 확인해보죠.

(좌변) = 1

(우변) = $\frac{n(n+1)(2n+1)}{6}$ = $\frac{1(1+1)(2 × 1 + 1)}{6}$ = 1

(좌변) = (우변)이므로 n = 1일 때 등식이 성립해요.

2. n = k일 때 등식이 성립하면 n = k + 1일 때도 성립하는지 확인해보죠.

1² + 2² + 3² + 4² + … + k²
    = $\frac{k(k+1)(2k+1)}{6}$
1² + 2² + 3² + 4² + … + k² + (k + 1)²
    = $\frac{k(k+1)(2k+1)}{6}$ + (k + 1)²
     (∵ 양변 + (k + 1)²)
1² + 2² + 3² + 4² + … + k² + (k + 1)²
    = $\frac{1}{6}$(k + 1){k(2k + 1) + 6(k + 1)}
1² + 2² + 3² + 4² + … + k² + (k + 1)²
    = $\frac{1}{6}$(k + 1)(2k² + 7k + 6)
1² + 2² + 3² + 4² + … + k² + (k + 1)²
    = $\frac{1}{6}$(k + 1)(k + 2)(2k + 3)
1² + 2² + 3² + 4² + … + k² + (k + 1)²
    = $\frac{1}{6}$(k + 1){(k + 1) + 1}{2(k + 1) + 1}

n = k + 1을 등식에 대입한 것과 같으므로 n = k + 1일 때도 등식이 성립해요.

따라서 이 등식은 모든 자연수 n에 대하여 성립해요.

모든 자연수 n이 아니라 m(m ≥ 2)보다 크거나 같은 자연수 n에 대하여 성립하는지를 증명할 때는 1. 기초단계에서 n = 1일 때가 아니라 n = m일 때로만 바꾸고 나머지는 똑같이 증명하면 돼요.

n ≥ 5인 자연수 n에 대하여 부등식 2ⁿ ≥ n²이 성립함을 수학적 귀납법을 이용하여 증명하여라.

1. n = 5일 때,

2⁵ = 32 ≥ 5² = 25

(좌변) ≥ (우변)이므로 n = 5일 때 부등식이 성립해요.

2. n = k (k ≥ 5)일 때 부등식이 성립하면 n = k + 1일 때도 성립하는지 확인해보죠.

2^k ≥ k²
2^k × 2 ≥ k² × 2         (∵ 양변 × 2)
2^k ≥ 2k²

2k² - (k + 1)²
= 2k² - k² - 2k - 1
= k² - 2k - 1
= (k - 2k + 1 - 1) - 1
= (k - 1)² - 2

k ≥ 5일 때, (k - 1)² - 2 ≥ 0이므로 2k² ≥ (k + 1)²

2^{k + 1} ≥ 2k² ≥ (k + 1)² → 2^{k + 1} ≥ (k + 1)²

n = k + 1을 부등식에 대입한 것과 같으므로 n = k + 1일 때도 부등식이 성립해요.

따라서 이 부등식은 n ≥ 5인 자연수에 대하여 성립해요.

수열의 귀납적 정의에 대해서 공부할 건데, 먼저 귀납이 무슨 뜻인지 부터 알아보죠.

귀납(歸納)에서 귀(歸)는 돌아올 귀인데, 돌아오다, 돌아가다의 뜻이에요. 밖에 나갔다가 집으로 돌아오는 걸 귀가라고 하고, 외국에 있다가 한국에 다시 들어오는 걸 귀국이라고 하죠?

납(納)은 들일 납인데, 들이다, 바치다, 받아들이다의 뜻이에요. 세금을 내는 걸 납세라고 하고, 은행 창구에서 돈을 받는 걸 수납이라고 하죠?

정리하면, 귀납은 “돌아가게 해서 받아들인다. → 개별적 사실들을 모아 받아들여 일반적 결론으로 돌아간다.”는 뜻으로 이해하면 돼요.

수열의 명시적 정의, 귀납적 정의

수열을 정의하는 방법에는 두 가지가 있어요.

첫 번째 방법은 a_n = 2n + 1처럼 a_n을 n에 대한 공식으로 직접 나타내는 방법으로 명시적 정의라고 해요. 이제까지 우리가 공부했던 방법이에요.

두 번째 방법은 반복되는 규칙을 관계식으로 나타내는 방법으로 귀납적 정의라고 해요. 처음 몇 개의 항과 이웃하는 항들과의 관계식을 이용해요.

a₁ = 1, a_{n + 1} = a_n + 2이라고 해보죠.

첫 번째 항은 1이에요. a₁ = 1이라서 첫 번째 항은 1이에요. a_{n + 1} = a_n + 2이니까다음 항은 바로 앞항보다 2만큼 큰 관계가 있어요. 결과적으로 이 수열은 첫째항이 1이고, 공차 2인 등차수열이에요.

a₁ = 2, a_{n + 1} = 3a_n일 때, a₁ = 2라서 첫째항이 2고 a_{n + 1} = 3a_n이니까 다음 항은 바로 앞항의 3배인 관계가 있어요. 즉, 첫째항이 2고 공비가 3인 등비수열이죠.

여기서 a_{n + 1} = a_n + 2와 a_{n + 1} = 3a_n처럼 이웃하는 항들 사이의 관계를 나타내는 식을 점화식이라고 해요.

등차수열과 등비수열의 귀납적 정의

등차수열, 등차수열의 일반항에서 첫째항이 a이고, 공차가 d인 등차수열은 a_n = a + (n - 1)d라고 했죠? 같은 등차수열을 귀납적으로 정의하면 수열 {a_n}이 첫째항이 a이고, 공차가 d인 등차수열일 때, a₁ = a, a_{n + 1} = a_n + d (n = 1, 2, 3, …)이라고 정의해요.

등차수열을 첫째항 a와 이웃하는 항(n항, n + 1항) 사이의 관계식으로 정의했잖아요.

등비수열, 등비수열의 일반항, 등비중항에서 첫째항이 a이고, 공비가 r인 등비수열은 a_n = ar^{n - 1}이었어요. 같은 등비수열을 귀납적으로 정의하면 수열 {a_n}이 첫째항이 a이고, 공비가 r인 등비수열일 때, a₁ = a, a_{n + 1} = ra_n (n = 1, 2, 3, …)이라고 정의해요.

등비수열도 등차수열과 마찬가지로 첫째항과 이웃하는 항 사이의 관계식을 이용했어요.

여러 가지 점화식

이웃하는 항들 사이의 관계를 나타내는 식(점화식)을 보면 이 수열이 등차수열인지 등비수열인지 알 수 있어요.

(1) a_{n + 1} = a_n + d → a_{n + 1} - a_n = d(일정) → 공차가 d인 등차수열
(2) a_{n + 1} = raⁿ → a_{n + 1} ÷ a_n = r(일정) → 공비가 r인 등비수열
(3) a_{n + 1} - a_n = a_{n + 2} - a_{n + 1} → 2a_{n + 1} = a_n + a_{n + 2} → 등차수열
(4) a_{n + 1} ÷ a_n = a_{n + 2} ÷ a_{n + 1} → (a_{n + 1})² = a_n × a_{n + 2} → 등비수열

다음과 같이 귀납적으로 정의된 수열 {a_n}의 일반항을 구하시오. (단, n = 1, 2, 3, …)
(1) a₁ = 3, a₂ = 6, a_{n + 1} = a_n + 3
(2) a₁ = 3, a₂ = 6, (a_{n + 1})² = a_n × a_{n + 2}

(1) a₁ = 3이고, a_{n + 1} = a_n + 3이므로 이 수열은 첫째항이 3이고, 공차가 3인 등차수열이에요.

첫째항이 a, 등차가 d인 등차수열의 일반항은 a_n = a + (n - 1)d예요. 공식에 넣어보죠.

a_n = 3 + (n - 1)3 = 3n

(2) a₁ = 3, (a_{n + 1})² = a_n × a_{n + 2}이므로 이 수열은 첫째항이 3인 등비수열이에요.

공비를 구해야겠네요.

r = $\frac{a_{2}}{a_{1}}$ = $\frac{6}{3}$ = 2

첫째항이 a, 등비가 r인 등비수열의 일반항은 a_n = ar^{n - 1}이에요. 공식에 넣어보죠.

a_n = 3 × 2^{n - 1}

일반항이 분수꼴인 수열의 합

부분분수

부분분수는 분수의 분모를 다항식의 곱으로 나타내고, 이를 이용해서 분수를 나누는 걸 말해요. 그냥 둬도 되는데 굳이 나누는 이유는 분자, 분모의 차수를 낮출 수 있어서예요. 차수가 낮거나 숫자가 작으면 계산하기 편리해지잖아요.

앞으로 분모가 인수분해가 되면 좌변을 우변처럼 바꿔서 계산하세요.

분자는 다 1인데, 좌변의 분모는 분모의 곱 AB, 우변 앞은 분모의 차 B - A, 괄호 안은 분수의 빼기에요. 빼는 순서도 잘 보세요.

부분분수 공식을 유도해볼까요? 분자, 분모에 같은 수를 곱해도 값은 바뀌지 않죠? 그걸 이용하는 겁니다.

숫자를 넣어서 좀 쉬운 걸 한 번 해보죠.

부분분수 공식을 이용하면 분모가 연속된 숫자나 식의 곱으로 이루어진 다항식들의 합을 구하기가 쉬워요. 아래 예제를 보죠.

다음을 간단히 하여라.$$\frac{1}{(x+1)(x+2)} + \frac{1}{(x+2)(x+3)} + \frac{3}{(x+1)(x+4)} +\cdots \frac{1}{(x+9)(x+10)}$$

유리식의 덧셈은 분모를 통분해서 구하는데, 앞 식을 통분하면 분모는 10차식 분자는 8차식이 돼요. 전개하고 더할 수는 없겠죠? 이럴 때 부분분수 공식을 이용해요..

각 항을 부분분수로 바꿔보죠.

우변의 괄호 앞에 있는 분수는 1이니까 없어지고 괄호 안 부분만 남겠죠? 이걸 한 번에 쭉 써보죠.

윗줄에서 두 번째, 세 번째 항이 없어지고, 네 번째, 다섯 번째 항이 없어지고, 계속 없어지다가 결국에는 첫 번째 항과 마지막 항만 남아요. 두 항의 덧셈만 하면 끝이죠.

앞으로는 이런 문제가 나오면 위 과정을 다 거칠 필요 없이 첫 번째 항과 마지막 항만 바로 구해서 계산하면 돼요.

분자가 1이 아닐 때도 있는데, 이럴 때는 분자를 인수분해해서 묶으면 돼요.

분모가 1이 아닐 때도 마찬가지로 묶고요.

다음 합을 구하여라. $$\frac{1}{1\times 2} + \frac{1}{2\times 3}+\frac{1}{3\times 4}+\cdots+\frac{1}{9\times 10}$$

분모가 유리식인 수열의 합이네요. 수열의 일반항을 이용해서 수열의 합으로 나타내고, 수열의 일반항인 분수를 쪼개(?) 보죠.

일반항이 무리식인 수열의 합

유리식은 통분해서 계산하는 게 기본이죠. 하지만 앞서 일반항이 유리식일 때 수열의 합을 구하는 문제는 통분이 아니라 분수를 쪼개서(?) 계산했어요.

무리식은 분모의 유리화를 하는 게 기본이죠. 이건 다르지 않아요. 일반항이 무리식이라면 분모를 유리화하는 게 첫 번째예요.

다음 합을 구하여라. $$\frac{1}{1+\sqrt{2}}+\frac{1}{\sqrt{2}+\sqrt{3}}+\frac{1}{\sqrt{3}+\sqrt{4}}+\cdots+\frac{1}{\sqrt{9}+\sqrt{10}}$$

분모가 무리식인 수열의 합이네요. 수열의 일반항을 이용해서 수열의 합으로 나타내고, 수열의 일반항의 분모를 유리화해요.

중학교 2학년 때 공부했던 삼각형의 외심 기억하죠? 이번에는 삼각형 외심의 좌표를 구해볼까요?

삼각형 외심의 좌표는 2가지 방법으로 구할 수 있어요.

첫번째는 외심의 정의를 이용하는 방법이에요. 두번째는 외심의 성질을 이용하는 방법이고요.

삼각형 외심의 좌표 구하기 - 외심의 정의 이용

첫번째 외심의 정의를 이용해서 외심의 좌표를 구해보죠.

삼각형의 외심은 세 변의 수직이등분선의 교점이에요. 물론, 세 변의 수직이등분선을 다 구하지 않고, 두 변의 수직이등분선의 교점만 구해도 돼요.

여기서는 변의 수직이등분선이라는 게 결정적인 힌트에요. 일단 삼각형에서 두 변의 방정식을 각각 구하고, 이 두 변과 수직이등분선의 방정식을 구해서 이 두 방정식의 교점을 찾는 거예요. 어려워보이죠? 하지만 생각보다 더 어려울 거예요.

좌표 위에 세 점 A(x₁, y₁), B(x₂, y₂), C(x₃, y₃)를 꼭짓점으로 하는 △ABC의 외심의 좌표를 구해보죠.

1단계, 두 변의 방정식을 각각 구해야하는데, 두 점을 지나는 직선의 방정식을 공식을 이용해서 구할 수 있어요.

$$ \overline{AB}의 방정식: y - y_{1} = \frac{y_{2} - y_{1}}{x_{2} - x_{1}} (x - x_{1})\\ 중점: \left( \frac{x_{1} + x_{2}}{2}, \frac{y_{1} + y_{2}}{2} \right)$$ $$ \overline{BC}의 방정식: y - y_{2} = \frac{y_{3} - y_{2}}{x_{3} - x_{2}} (x - x_{2})\\ 중점: \left( \frac{x_{2} + x_{3}}{2}, \frac{y_{2} + y_{3}}{2} \right)$$

2단계, 각 변의 수직이등분선의 방정식을 구해보죠.

$\overline{AB}$의 방정식과 중점을 구했으니, 여기에 수직이등분선의 직선의 방정식을 구할 수 있죠? 두 직선이 서로 수직이면 기울의 곱 = -1이에요. $$ \frac{y_{2} - y_{1}}{x_{2} - x_{1}} \times 기울기 = -1\\ 기울기 = - \frac{x_{2} - x_{1}}{y_{2} - y_{1}}$$

이 직선은 $\overline{AB}$의 중점을 지나니까 기울기와 한 점의 좌표를 알 때 직선의 방정식 구하는 공식으로 구할 수 있어요.

$$ y - \frac{y_{1} + y_{2}}{2} = - \frac{x_{2} - x_{1}}{y_{2} - y_{1}} \left( x - \frac{x_{1} + x_{2}}{2} \right)$$

같은 방법으로 $\overline{BC}$의 수직이등분선의 방정식을 구할 수 있죠?

$$ \frac{y_{3} - y_{2}}{x_{3} - x_{2}} \times 기울기 = -1\\ 기울기 = - \frac{x_{3} - x_{2}}{y_{3} - y_{2}}$$

이 직선은 $\overline{BC}$의 중점을 지나요.

$$ y - \frac{y_{2} + y_{3}}{2} = - \frac{x_{3} - x_{2}}{y_{3} - y_{2}} \left( x - \frac{x_{2} + x_{3}}{2} \right)$$

3단계, 연립방정식을 이용해서 이 두 직선의 교점을 구하면 바로 외심의 좌표예요.

이 이후의 과정은 너무 복잡하니까 그냥 구하지 말죠. 아무튼 순서를 잘 기억하세요.

1. 삼각형의 두 꼭짓점을 이용해서 변의 방정식과 중점을 구한다. × 2
2. 각 변의 수직이등분선의 방정식을 구한다.
3. 연립방정식을 이용하여 ②에서 구한 수직이등분선의 교점의 좌표를 구한다.

삼각형 외심의 자표구하기 - 외심의 성질 이용

두 번째 방법은 삼각형 외심의 성질을 이용하는 방법이에요.

삼각형 외심의 성질은 무엇이었나요? 외심에서 세 꼭짓점에 이르는 거리가 같잖아요. 그러니까 외심의 좌표를 점O(x, y)라고 놓고, 좌표평면에서 두 점 사이의 거리 공식을 이용해서 $\overline{OA} = \overline{OB} = \overline{OC}$ 를 구하는 거죠.

A = B = C꼴의 연립방정식이니까 A = B or B = C or C = A 중 2개를 골라서 연립방정식을 만들고 풀면 돼요.

진짜로 풀지는 말고, 그 방법만 알고 있으면 돼요.

결과는 이거예요. 심심하면 외워보세요.

$$x = \frac{ (x_1^2 + y_1^2)(y_2 - y_3) + (x_2^2 + y_2^2)(y_3 - y_1) + (x_3^2 + y_3^2)(y_1 - y_2) }{ 2 \cdot (x_1(y_2 - y_3) + x_2(y_3 - y_1) + x_3(y_1 - y_2))}\\\\ y = \frac{ (x_1^2 + y_1^2)(x_3 - x_2) + (x_2^2 + y_2^2)(x_1 - x_3) + (x_3^2 + y_3^2)(x_2 - x_1) }{ 2 \cdot (x_1(y_2 - y_3) + x_2(y_3 - y_1) + x_3(y_1 - y_2))}$$

분수함수 중에 $y\quad =\quad \frac{cx \quad + \quad d}{ax \quad + \quad b} $꼴의 함수가 있어요. 이 함수는 분자에서 일차항의 계수인 a ≠ 0이어야 하고, 식에 사용된 계수들이 ad - bc ≠ 0이어야 해요.

분자에서 일차항의 계수 a = 0이면 $y \quad = \quad \frac{c}{b}x\quad + \quad \frac{d}{b}$꼴로 계수가 유리수인 다항함수예요. 그래서 a ≠ 0이어야 해요.

ad - bc = 0이면 안되는 이유를 알아보죠.

$$ \begin{align}ad \quad - \quad bc \quad & = \quad 0\\ \\ ad \quad & = \quad bc\\ \\ d \quad & = \quad \frac{bc}{a} \end{align}$$

ad - bc = 0일 때, 먼저 bc를 이항해요. 그리고 앞에서 본 것처럼 a ≠ 0이니까 양변을 a로 나눴더니 d = $\frac{bc}{a}$가 됐어요.

이번에는 위에서 얻은 d = $\frac{bc}{a}$를 원래의 분수함수 $y\quad = \quad \frac{cx \quad + \quad d}{ax \quad + \quad b} $에 대입하고 분자, 분모를 각각 일차항의 계수로 묶어보죠.

$$ \begin{align} y \quad & = \quad \frac{cx \quad + \quad d}{ax \quad + \quad b} \\ \\ y \quad & = \quad \frac{cx \quad + \quad \frac{bc}{a}}{ax \quad + \quad b}\\ \\ y \quad & = \quad \frac{c \left(x\quad + \quad \frac{b}{a}\right)}{a \left(x \quad + \quad \frac{b}{a} \right)} \\ \\ y \quad & = \quad \frac{c}{a} \end{align}$$

괄호 부분을 약분했더니 y = $\frac{c}{a}$가 되었고, 이건 상수함수예요.

분모에 문자가 있어야 분수식이라고 하고, 함수식이 분수식이어야 분수함수인데, 이건 그냥 상수함수라서 다항함수예요. 그래서 분수함수에서는 ad - bc ≠ 0이라는 조건이 있어요.

수학적 귀류법은 어떤 명제가 참임을 증명하고 싶은데, 직접 증명하기 어려울 때 사용하는 간접 증명 방법이에요.

쉽게 말해 명제를 거짓이라고 가정했더니 말이 안된다(모순이 발생한다)는 걸 보임으로써 결국 그 명제가 참이라는 걸 증명하는 거예요.

수학적 귀류법은 다음의 3단계를 거쳐요.

1. 어떤 명제가 있는데, 이 명제가 거짓이라고 가정해요.
   증명하고 싶은 명제의 결론을 부정해서 가정으로 삼아요.
2. 가정에서 논리적 결론을 이끌어 내어, 모순이 생기는 걸 보여서, 가정이 틀렸다는 걸 확인해요.
   가정을 바탕으로 논리적으로 전개하다 보면 기존에 알려진 사실이나 정의에 모순되는 결과가 나오는 걸 보여줘요. 모순이 생겼으니 처음에 세웠던 가정이 거짓이에요.
3. 결국 원래 명제가 참이라는 결론에 도달해요.
   원래 증명하고 싶었던 명제가 참이라는 결론을 내려요.

예를 들어보죠. "김철수는 남자이다."를 증명해볼까요?

1. 명제가 거짓이라고 가정: 김철수는 남자가 아니다. → 김철수는 여자이다.
2. 모순: 여자는 OOO, ~~~ 같은 신체적, 생물학적 특징이 있어야 하는데, 김철수는 그런 특징이 없으므로 "김철수는 여자"라는 가정이 틀렸다.
3. 결론: 김철수는 여자가 아니다. → "김철수는 남자다."는 참이다.

"$\sqrt{2}$는 무리수"임을를 수학적 귀류법으로 증명하시오.

1. 명제가 거짓이라고 가정: $\sqrt{2}$는 무리수가 아니다. → $\sqrt{2}$는 유리수이다.
   유리수는 $\frac{a}{b}$ (a, b는 서로소인 정수, b ≠ 0) 꼴로 나타낼 수 있는 수예요.
2. $\sqrt{2}$ = $\frac{a}{b}$
     2 = $\frac{a^{2}}{ b^{2}}$           (∵양변 제곱)
   2b² = a²
   
   a²이 2의 배수니까 a도 2의 배수여야 해요. 따라서 a = 2k (k는 정수)라고 둘 수 있어요.
   
   a = 2k를 2b² = a²에 대입하면
   2b² = a²
   2b² = (2k)²
   2b² = 4k²
   b² = 2k²
   
   b²도 2의 배수이므로 b도 2의 배수여야 해요.
   
   a, b 모두 2의 배수이므로 a, b는 서로소인 정수라고 했던 가정과 모순이 생겨요. 가정 "$\sqrt{2}$는 유리수"가 틀렸다는 걸 알 수 있어요.
3. 명제 "$\sqrt{2}$는 무리수이다."는 참인 명제예요.

명제 “모든 홀수는 짝수가 아니다.”를 귀류법으로 증명하시오.

명제를 부정해야 하는데, 조건의 부정에 나온 것처럼 "모든"은 "어떤"으로 바꿔요.

1. 명제가 거짓이라고 가정: 어떤 홀수가 짝수이다.
2. 홀수는 2n+1, 짝수는 2n (n은 정수)이므로 어떤 홀수가 짝수이면
   2n + 1 = 2m
   2n + 1 = 2m
   1 = 2m - 2n
   1 = 2(m - n)
   
   1이 2의 배수라는 결론이 나오는데, 이는 말이 안되죠. 모순이에요. 가정이 틀렸어요.
3. 모든 홀수는 짝수가 아니다. (명제는 참이다)

이차방정식의 판별식을 이용해서 두 근이 실근인지 허근인지 판별할 수 있어요. 이번에 공부할 건 조금 확장된 버전(?)인데요. 교육과정에 있는 내용은 아닌데, 그냥 한 번 해보죠.

이차방정식은 모르지만, 이차방정식 두 근의 합과 곱을 알 때, 두 근이 실근인지 허근인지 확인하는 방법이에요. 판별식을 이용하는 방법보다 한 단계만 더 거치는 거니까 어렵지는 않아요.

식을 알면 두 근을 구해서 실근인지 허근이지 판별할 수 있는데, 식을 모르니까 두 근을 구할 수 없고, 근을 모르니까 실근인지 허근인지 판별할 수 없어요.

하지만, 이차방정식의 판별식, 실근, 허근에서도 근을 구하지 않고 실근, 허근을 판별했어요. 즉, 식을 알기만 하면 근을 구할 수 없을더라도 실근, 허근을 판별할 수는 있어요.

판별식을 이용하려면 식을 알아야 하죠. 그런데 식을 몰라요. 합과 곱만 알아요. 어떻게 해야 할까요? 식을 먼저 구해야겠죠? 식을 구하는 방법이 뭘까요? 바로 두 수를 근으로 하는 이차방정식, 두 근의 합과 곱이 주어졌을 때 이차방정식이에요.

그러니까 합과 곱을 이용해서 이차방정식을 만들고, 그렇게 만든 이차방정식에서 판별식을 구하면 두 근이 실근인지 허근인지 확인할 수 있어요.

두 근의 합과 곱을 알 때 이차방정식은 다음과 같아요.

두 근의 합이 m이고 곱이 n, 이차항의 계수가 a인 이차방정식
a(x² - mx + n) = 0
a(x² - 합x + 곱) = 0

위 공식을 전개해보면 ax² - amx + an = 0이에요.

나머지 과정은 다 알죠?

D = (-am)² -  4  × a  ×   an

• D > 0이면 서로 다른 두 실근
• D = 0이면 중근(실근)
• D < 0이면 서로 다른 두 허근

두 근의 합이 9, 곱이 18이고 이차항의 계수가 2인 이차방정식의 근의 종류를 판별하여라.

근이 뭔지는 모르지만, 두 근의 합과 곱, 이차항의 계수를 알려줬네요. 식을 구할 수 있어요.

a(x² - 합x + 곱) = 0

2(x²  +  9x +  18)  =  0
2x² + 18x + 36 = 0

이제 식을 알았으니 판별식을 사용할 수 있어요.

D/4 = 9² - 2 × 36
= 81 - 72
= 9 > 0

D/4 > 0이니까 서로 다른 두 실근이에요.

여기서 한 가지 더 알아둘 건, 이차항의 계수는 별 필요가 없다는 거예요.

합이 m, 곱이 n, 이차항의 계수가 a인 이차방정식
a(x - mx + n) = 0
ax² - amx + an = 0

D = (-am)² - 4 × a × an
= a²m² - 4a²n
= a²(m² - 4n)

a²은 무조건 양수니까 뒤 (m² - 4n)의 부호만 알면되죠?

이차항의 계수 없이 공식의 괄호부분만 볼까요?

x² - mx + n = 0

D = (-m)² - 4 × 1 × an
= m² - 4n

결국 이차항의 계수는 판별식의 부호에 아무런 영향을 미치지 않아요.

2015 교육과정 수학 1과 2022 교육과정 대수가 목차가 같아 하나로 작성하였습니다.

각 게시글 하단의 목차 페이지는 이용하지 말고, 이 목차 페이지에서 필요한 단원의 글만 골라서 공부하세요.

대수

1. 지수함수와 로그함수
   • 거듭제곱근
   • 실수인 거듭제곱근
   • 거듭제곱근의 성질
   • 지수의 확장 - 정수 지수
   • 지수의 확장 - 유리수 지수
   • 지수의 확장 - 실수 지수
   • 지수함수와 그 그래프
   • 지수함수 그래프의 평행이동
   • 지수방정식과 풀이
   • 지수부등식과 풀이
   • 로그의 정의
   • 로그의 성질
   • 로그의 밑 변환 공식
   • 로그의 성질 두 번재 - 밑 변환 공식 이용
   • 상용로그, 상용로그의 지표와 가수
   • 상용로그표, 비례부분의 법칙
   • 상용로그의 활용 - 단리와 복기
   • 로그함수와 그래프
   • 로그함수 그래프의 평행이동
   • 로그방정식
   • 로그부등식
2. 삼각함수
   • 일반각, 시초선, 동경, 양의 각, 음의 각, 사분면의 각
   • 호도법과 라디안
   • 부채꼴 호의 길이와 넓이
   • 삼각함수의 뜻과 정의, sin, cos, tan
   • 삼각함수 사이의 관계
   • 삼각함수 각의 변환 1 - 2nπ ± θ, -θ
   • 삼각함수 각의 변한 2 - π ± θ, π/2 ± θ
   • 삼각함수 각의 변환 총정리
   • 삼각함수표
   • 삼각함수의 그래프 - sin 그래프
   • 삼각함수의 그래프 - cos 그래프
   • 삼각함수의 그래프 - tan 그래프
   • 삼각함수 그래프의 이동, 평행이동, 주기, 최대, 최소
   • 삼각함수를 포함한 식의 최댓값과 최솟값
   • 삼각방정식
   • 삼각부등식
   • 사인법칙, 사인법칙 증명
   • 제1 코사인법칙, 제1 코사인법칙 증명
   • 제2 코사인법칙, 제2 코사인법칙 증명
   • 사인법칙, 코사인법칙 총정리
   • 삼각형의 넓이
   • 헤론의 공식
   • 평행사변형의 넓이, 사각형의 넓이
3. 수열
   • 수열의 뜻
   • 등차수열, 등차수열의 일반항
   • 등차수열 일반항의 성질, 등차중항
   • 등차수열의 합 공식
   • 등차수열의 합과 등차수열 일반항의 관계
   • 조화수열, 조화중항
   • 등비수열, 등비수열의 일반항, 등비중항
   • 등비수열의 합 공식
   • 등비수열의 합과 등비수열 일반항의 관계
   • 수열의 활용 - 원리합계, 단리
   • 수열의 활용 - 원리합계, 복리
   • 여러 가지 수열의 합, 시그마(∑)
   • 시그마(∑)의 기본 성질
   • 자연수 거듭제곱의 합 공식, 유도
   • 여러 가지 수열
   • 수학적 귀납법

각 게시글 하단의 목차 페이지는 이용하지 말고, 이 목차 페이지에서 필요한 단원의 글만 골라서 공부하세요.

공통수학 1

1. 다항식
   • 다항식의 덧셈과 뺄셈, 곱셈
   • 곱셈공식
   • 곱셈공식의 변형
   • 다항식의 나눗셈
   • 항등식과 항등식의 성질
   • 미정계수법 - 계수비교법, 수치대입법
   • 나머지정리, 인수정리
   • 조립제법 1 - 조립제법 하는 법
   • 조립제법 2 - 나누는 식의 x의 계수가 1이 아닐 때
   • 인수분해 공식
   • 복잡한 식의 인수분해 - 치환, 복이차식
   • 인수정리를 이용한 인수분해
2. 방정식과 부등식
   • 허수와 허수단위, 복소수
   • 켤레복소수와 켤레복소수의 성질
   • 복소수의 사칙연산
   • i의 거듭제곱, 음수의 제곱근의 성질
   • 방정식 ax + b = 0의 풀이, 부정, 불능
   • 절댓값 기호를 포함한 일차방정식의 풀이
   • 이차방정식의 판별식, 실근, 허근
   • 이차방정식 근과 계수와의 관계
   • 두 수를 근으로하는 이차방정식, 두 근의 합과 곱이 주어졌을 때 이차방정식
   • 이차방정식의 켤레근
   • 이차방정식의 인수분해
   • 이차방정식의 실근의 부호
   • 이차함수 총정리
   • 이차함수의 최댓값과 최솟값
   • 이차함수의 최대, 최소와 활용
   • 이차함수의 그래프와 이차방정식의 실근
   • 이차함수의 그래프와 직선의 위치관계
   • 이차방정식의 실근의 위치
   • 고차방정식의 인수분해, 고차방정식의 풀이
   • 고차방정식의 풀이 - 치환, 복이차식
   • 삼차방정식 근과 계수와의 관계
   • 삼차방정식의 허근 ω의 성질
   • 연립이차방정식의 풀이 1
   • 연립이차방정식의 풀이 2 - 대칭식
   • 부등식의 성질
   • 부등식 ax > b의 풀이, 부정, 불능
   • 연립부등식
   • 여러가지 연립부등식
   • 절댓값 기호를 포함한 일차부등식의 풀이
   • 절댓값 기호를 포함한 부등식의 풀이 2
   • 이차부등식, 이차부등식의 해
   • 이차부등식의 해와 판별식
   • 이차부등식의 해와 이차함수의 그래프
   • 해가 주어졌을 때 이차부등식 구하기
   • 이차부등식이 항상 성립할 조건
   • 연립이차부등식
3. 순열과 조합
   • 합의 법칙, 곱의 법칙
   • 순열이란
   • 계승, 팩토리얼(!)
   • 순열의 활용
   • 조합이란
   • 조합의 성질
   • 조합의 활용
4. 행렬
   • 행렬, 행렬의 뜻, 정사각행렬
   • 행렬의 성분, 두 행렬이 서로 같을 조건
   • 행렬의 덧셈과 뺄셈, 행렬의 덧셈에 대한 성질
   • 영행렬
   • 행렬의 실수배, 행렬의 실수배에 대한 성질
   • 행렬의 곱셈, 행렬의 거듭제곱
   • 행렬의 곱셈에 대한 성질
   • 단위행렬

공통수학 2

1. 도형의 방정식
   • 두 점 사이의 거리
   • 선분의 내분점과 외분점
   • 좌표평면 위의 내분점과 외분점
   • 내분점과 외분점의 관계
   • 삼각형 무게중심의 좌표
   • 직선의 방정식, 직선의 방정식 구하기
   • 직선의 방정식 일반형과 표준형
   • 절댓값 기호를 포함한 식의 그래프
   • 두 직선의 위치관계 - 평행, 일치, 수직
   • 두 직선의 위치관계와 일차방정식의 해의 개수
   • 교점을 지나는 직선의 방정식
   • 점과 직선 사이의 거리
   • 원의 방정식
   • 원의 방정식 일반형과 표준형
   • 아폴로니오스의 원
   • 축에 접하는 원의 방정식
   • 두 원의 교점을 지나는 원의 방정식
   • 원과 직선의 위치관계
   • 원의 접선의 방정식 1 - 접점을 알 때
   • 원의 접선의 방정식 2 - 기울기를 알 때
   • 원의 접선의 방정식 3 - 원 밖의 한 점에서 그은 접선의 방정식
   • 점과 도형의 평행이동
   • 점과 도형의 대칭이동 - x축, y축, 원점
   • 점과 도형의 대칭이동 - 직선에 대한 대칭이동
2. 집합과 명제
   • 집합의 뜻
   • 집합에서 원소란π
   • 집합의 표현방법 - 조건제시법, 원소나열법, 벤다이어그램
   • 집합의 분류 - 원소개수에 따른 분류(무한집합, 유한집합, 공집합)
   • 집합의 원소의 개수
   • 집합의 포함관계 - 부분집합
   • 진부분집합과 부분집합의 성질
   • 부분집합 구하기, 부분집합의 개수 구하기
   • 특정한 원소를 포함하는 부분집합의 개수 구하기
   • 교집합과 합집합
   • 전체집합과 여집합, 차집합
   • 집합의 연산법칙 - 교환법칙, 결합법칙, 분배법칙
   • 집합의 연산법칙 - 드모르간의 법칙
   • 유한집합의 원소의 개수
   • 명제와 조건, 진리집합, 조건의 부정
   • 명제의 참, 거짓
   • 명제의 역, 이, 대우, 삼단논법
   • 필요조건, 충분조건, 필요충분조건
   • 수학에서의 정의, 증명, 정리
   • 절대부등식, 부등식의 증명에 사용되는 실수의 성질
   • 절대부등식의 증명 - 산술, 기하, 조화평균
   • 절대부등식의 증명 - 코시 슈바르cm 부등식
3. 함수
   • 함수의 정의
   • 정의역, 공역, 치역, 서로 같은 함수
   • 함수의 그래프
   • 일대일 대응, 일대일함수
   • 합성함수
   • 합성함수의 성질
   • 역함수, 역함수 구하는 방법
   • 역함수의 성질과 그래프
   • 유리식, 분수식, 유리식의 사칙연산
   • 여러가지 유리식의 풀이
   • 유리함수
   • 유리함수 2 - 분수함수
   • 분수함수의 역함수
   • 무리식, 무리식의 연산
   • 무리함수
   • 무리함수 2
   • 무리함수의 역함수

이번에 공부할 연립이차방정식은 대칭식인데요. 연립이차방정식에서는 x, y라는 두 개의 미지수를 사용하죠? 이때, x와 y의 자리를 바꿔도 원래의 식과 같아지는 식을 대칭식이라고 해요.

$\left\{\begin{matrix} x + y + xy = 7 \\x^2 + 3xy + y^2 = 19 \end{matrix}\right. \rightarrow \left\{\begin{matrix}y + x + yx = 7\\y^2 + 3yx + x^2 = 19\end{matrix}\right. $

왼쪽의 x와 y를 서로 바꿨더니 오른쪽처럼 되었어요. 그런데 두 식이 똑같죠? 이런 경우를 대칭식이라고 해요.

이런 식은 x + y = u, xy = v라고 치환해서 풀어요.

$\left\{\begin{matrix} x + y + xy = 7 \\x^2 + 3xy + y^2 = 19 \end{matrix}\right. \rightarrow \left\{\begin{matrix}u + v = 7\\u^2 + v = 19\end{matrix}\right. $

(∵ x² + 3xy + y² = (x + y)² + xy)

치환을 했더니 x, y에 대한 연립이차방정식이 u, v에 대한 연립이차방정식으로 바뀌었죠? 첫 번째 식은 1차식, 두 번째 식은 2차식이에요. 앞서 공부했던 (일차방정식 + 이차방정식)꼴의 연립이차방정식이므로 일차방정식을 한 문자에 대해 정리해서 이차방정식에 대입해서 풀면 되겠네요.

v = 7 ? u
u² + (7 ? u) = 19
u² ? u ? 12 = 0
(u ? 4)(u + 3) = 0
u = -3 or 4
v = 10 or 3

우리가 구해야 하는 건 u, v가 아니라 x, y잖아요. 원래 값으로 바꾸면
x + y = -3, xy = 10
x + y= 4, xy = 3

더해서 4 곱해서 3이 되는 두 수를 구하는 건데, 합과 곱이 주어졌을 때 이차방정식 구하기에 따라 식으로 만들면 x² ? 합x + 곱 = 0꼴이니
t² - 4t + 3 = 0

그냥 평범한 이차방정식으로 나타낼 수 있어요. 이 이차방정식을 풀면 돼요.

(t - 1)(t - 3)= 0
t = 1 or 3
x = 1, y = 3 or x = 3, y = 1

t² + 3t + 10 = 0
t = $\frac{-3 \pm \sqrt{3^2 - 4 \times 1 \times 10} }{2} = \frac{-3 \pm \sqrt{31}i }{2}$
x = $\frac{-3 + \sqrt{31}i}{2}$, y = $\frac{-3 - \sqrt{31}i }{2}$ or x = $\frac{-3 - \sqrt{31}i }{2}$, y = $\frac{-3 + \sqrt{31}i }{2}$

$$\left\{\begin{matrix} x = 1\\y = 3 \end{matrix}\right. , \left\{\begin{matrix} x = 3\\y = 1 \end{matrix}\right. , \left\{\begin{matrix} x = \frac{-3 + \sqrt{31}i}{2}\\ y = \frac{-3 - \sqrt{31}i}{2} \end{matrix}\right. , \left\{\begin{matrix} x = \frac{-3 - \sqrt{31}i}{2}\\y = \frac{-3 + \sqrt{31}i}{2} \end{matrix}\right.$$

이 풀이는 문자도 많이 나오고, 식이 바뀌는 부분이 많아 헷갈릴 수 있으니 주의해야 해요. 이 변화를 잘 파악해야 합니다.

x , y의 연립이차방정식 → u, v의 연립이차방정식 → t의 이차방정식 → x, y의 값

인수정리를 이용한 인수분해에서 인수정리에 사용할 α를 찾는 방벙 중 2번째 방법에 대해서 설명하는 글이에요.

α를 찾을 때 $\pm\frac{상수항의 \quad약수}{최고차항 \quad계수의\quad 약수}$ 중 하나라고 했는데 그 이유는 어렵지 않아요.

먼저, 간단한 거 하나만 보죠.

3 × 4 = 12라는 식에서 3, 4가 12의 약수라는 걸 알 수 있어요. 이때, 12의 약수는 1, 2, 3, 4, 6, 12인데 저 식에서는 나머지 약수는 알 수 없고 3, 4만 알 수 있죠.

다시 방정식으로 돌아와서, 최고차항이 a (a ≠ 0)이고, 세 근이 α, β, γ인 3차방정식이 있다고 해보죠.

ax³ + bx² + cx + d = 0
a(x - α)(x - β)(x - γ) = 0
a{x³ - (α + β + γ)x² + (αβ + βγ + γα)x - αβγ} = 0
ax³ - a(α + β + γ)x² + a(αβ + βγ + γα)x - aαβγ = 0

삼차방정식 근과 계수와의 관계에 따르면 αβγ = -$\frac{d}{a}$예요.

세근의 곱 = $\frac{상수항}{최고차항의\quad계수}$이죠. 앞의 부호는 신경쓰지 말고요.

3 × 4 = 12 → 3, 4는 12의 약수.
αβγ = $\frac{상수항}{최고차항의\quad계수}$ → α, β, γ는 $\frac{상수항}{최고차항의\quad계수}$의 약수

12의 약수 1, 2, 3, 4, 6, 12 중에 3, 4가 있죠? 마찬가지로 $\frac{상수항}{최고차항의\quad계수}$의 약수도 많이 있을텐데 그 중에 α, β, γ가 있어요. 우리는 α, β, γ만 필요하니까 어떤 것이 α, β, γ인지 찾아야 해요.

그 방법은 $\pm\frac{상수항의 \quad약수}{최고차항 \quad계수의\quad 약수}$로 찾은 약수를 하나씩 대입해서 방정식이 성립하는지 보는 거예요. 식이 성립하면 α, β, γ중 하나고, 성립하지 않으면 α, β, γ가 아닌 다른 약수죠, 

방정식의 해는 정수, 유리수, 무리수까지 있지만 우리는 계산을 쉽게 하려고 정수 약수만 찾을 거니까 여러 후보 중에서 정수만 먼저 대입해서 찾아요.

근을 모두 찾을 필요는 없고, 정수인 근 1, 2개만 찾아요. 정수가 아닌 근이 있다면 찾기가 어려울 수 있으니까요.

나머지는 조립제법을 이용하거나 인수분해 공식을 이용해서 인수분해를 하면 자연히 알게 돼요.

이건 3차방정식 뿐 아니라 4차, 5차 등 다른 방정식에서도 똑같아요. 어차피 방정식의 상수항은 근의 곱으로 된 항이니까요. 부호는 생각하지 말고요. 어차피 약수를 구할 때 앞에 $\pm$이 있으니까 부호는 상관없죠.