이차방정식의 근과 계수와의 관계

이차방정식의 근과 계수와의 관계는 중3 때 근과 계수와의 관계에서 했어요. 내용은 전혀 달라지지 않았습니다. 완전히 똑같아요. 대신 이걸 활용하는 문제가 조금 더 어려워진 것뿐이에요.

근과 계수와의 관계 공식을 잊어버렸다면 이 글을 통해서 한번 더 복습하고 앞으로는 잊어버리지 않도록 하세요.

이차방정식의 근과 계수와의 관계 문제에서는 곱셈공식의 변형을 이용한 문제들이 많이 나오니까 이 공식들도 기억하고 있어야 해요.

이차방정식의 근과 계수와의 관계

이차방정식 ax² + bx + c = 0 (a ≠ 0)의 근은 근의 공식을 이용해서 구할 수 있어요.

이차방정식의 두 근을 α, β라고 하고  , 라고 해보죠.

두 근의 합과 계수와의 관계

일단 두 근 α, β를 더 해보죠.

두 근의 곱과 계수와의 관계

이번에는 두 근을 곱해볼게요.

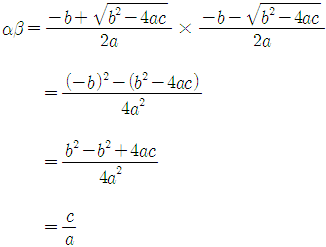
정리해보면 아래 공식을 얻을 수 있어요.

ax² + bx + c = 0 (a ≠ 0)
α + β = -$\frac{b}{a}$    αβ = $\frac{c}{a}$

두 근의 차와 계수와의 관계

이번에는 차를 구해보죠. 차는 α, β 중 어느 것이 더 큰지 모르니까 절댓값을 이용해서 구해요.

분자는 근의 공식에서 뒤에 있는 제곱근 부분으로 판별식 D에 루트 씌워놓은 거고, 분모는 |a|네요.

위 공식을 이용해서 차를 구하는 경우보다는, 두 근의 합(α + β)와 두 근의 곱(αβ)를 이용해서 구하는 경우가 훨씬 많아요. 이때, 곱셈공식의 변형을 사용해요.

2x² + 4x - 8 = 0의 두 근을 α, β라고 할 때 다음을 구하여라.
(1) α + β
(2) αβ
(3) α² + β²
(4) (α + 1)(β + 1)
(5)
(6) |α - β|

(1) α + β =

(2) αβ =

(3) α² + β²은 곱셈공식의 변형을 이용한 문제예요.
α² + β²
= (α + β)² - 2αβ
= (-2)² - 2 × (-4)
= 4 + 8 = 12

(4) (α + 1)(β + 1)는 곱셈공식을 이용해서 전개해야겠네요.
(α + 1)(β + 1)
= αβ + α + β + 1
= -4 + (-2) + 1
= -5

(5) 는 통분해서 계산해보죠.

(6) 두 근의 차는 두 근의 합, 두 근의 곱, 곱셈공식의 변형을 이용해서 구하고, 절댓값으로 표현합니다.
(α - β)² = (α + β)² - 4αβ
(α - β)² = (-2)² - 4 × (-4)
(α - β)² = 4 + 16
(α - β)² = 20
|α - β| = 

함께 보면 좋은 글

곱셈공식의 변형, 곱셈공식의 변형 유도
이차방정식의 판별식, 실근, 허근
[중등수학/중3 수학] - 근의 공식, 근의 공식 유도, 짝수 공식
[중등수학/중3 수학] - 근과 계수와의 관계

정리해볼까요

이차방정식 ax² + bx + c = 0(a, b, c는 실수, a≠ 0)에서 두 근을 α, β라고 할 때

• α + β =
• αβ =
• |α - β| ← (α - β)² = (α + β)² - 4αβ

이차방정식의 판별식, 실근, 중근, 허근

<<  수학 1 목차  >>

두 수를 근으로 하는 이차방정식

 

그리드형(광고전용)