함수, 함수의 정의, 대응
함수는 중학교에서 3년 내내 공부했던 거예요. 함수, 일차함수, 이차함수 그리고 그래프를 공부했었죠? 근데, 기억이 잘 안 나죠? 그래서 이 글에서는 함수의 뜻을 처음부터 다시 정리해볼 거예요.
용어의 의미만 제대로 파악하고 있어도 반은 먹고 들어가는 겁니다. 원소의 의미와 그림을 함께 연결지어서 생각하면 이해하기가 훨씬 쉬울 거예요.
함수는 지난 3년 동안 계속 공부해왔던 것처럼 앞으로 3년 동안 계속 공부할 거니까 이번 기회에 확실히 정리해 놓으세요.
함수
두 집합 X, Y가 있을 때, X의 원소와 Y의 원소를 짝을 지어주는 걸 대응이라고 해요. 대응변, 대응각 들어봤죠? X의 원소 x가 Y의 원소 y와 짝지어질 때, x에 y가 대응한다고 하고 기호로는 x → y라고 나타내요.
두 집합 X, Y에서 집합 X의 각 원소에 대하여 집합 Y의 원소가 하나씩만 대응할 때, 이 대응을 집합 X에서 집합 Y로의 함수라고 하며, 이것을 기호로 f: X → Y라고 나타내요. f는 영어단어 function의 첫 글자 f를 의미합니다.
함수가 되기 위해서는 몇 가지 조건을 만족해야 해요. 첫 번째로 집합 X의 한 원소 x에 집합 Y의 원소 중 하나만 대응해야 해요. 집합 X의 원소에 집합 Y의 원소가 여러 개 대응하면 안 돼요.
두 번째는 집합 X의 모든 원소에 집합 Y의 원소가 대응해야 합니다. 집합 X의 원소 중 집합 Y의 원소와 대응하지 않는 원소가 있으면 안 돼요.
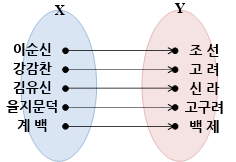
X는 이순신, 강감찬, 김유신, 을지문덕, 계백 원소를 가진 집합이고, Y는 조선, 고려, 신라, 고구려, 백제라는 나라 이름을 원소로 가진 집합이에요.
X에 있는 위인들을 Y에 있는 나라와 연결해봤더니 한 사람에 한 나라씩 대응하죠? 그래서 이 경우는 함수예요.

이번에도 마찬가지로 X에는 사람, Y에는 나라 이름을 연결했어요. 이순신, 김시민, 권율에는 조선이, 온달, 을지문덕에는 고구려가 대응해요. Y에 있는 고려, 신라, 백제에는 대응하는 게 없어요. 하지만 X의 모든 원소에 Y의 원소들이 하나씩 대응하고 있으니까 이 경우도 함수에요.
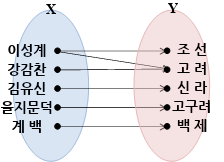
X의 이성계에 Y의 조선과 고려 두 개가 대응하죠. X의 원소에 Y의 원소가 하나만 대응해야 하는데, 그렇지 않으므로 이 경우는 함수가 아니에요. 이성계는 고려 시대에 살다가 조선을 건국했으니까 양쪽 모두에 대응하도록 연결했어요.
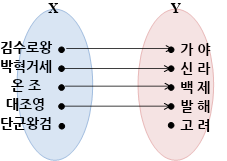
X의 원소들에 Y의 원소들이 하나씩 대응하고 있어요. 그런데 X의 원소 중 단군왕검은 Y의 원소와 대응하고 있지 않죠? X에 대응하지 않은 원소가 있으므로 이 경우도 함수가 아닙니다.
함께 보면 좋은 글
[중등수학/중1 수학] - 함수의 뜻과 함숫값, 함수의 정의
[중등수학/중2 수학] - 일차함수 뜻, 정의역, 공역, 치역
[중등수학/중3 수학] - 이차함수의 뜻, 이차함수란?