고등수학/고1 수학
정의역, 공역, 치역, 함숫값, 서로 같은 함수
함수의 정의에 이어 함수에서 사용하는 용어에 대해서 알아보죠. 정의역, 공역, 치역인데 들어본 적이 있을 거예요. 그냥 한 번 복습하는 차원에서 다뤄보죠.
용어의 정의에 대한 내용이니 외우기보다는 그 뜻을 잘 이해하는 게 중요해요. 사실 별 중요한 뜻이 있는 건 아니지만, 나중에 헷갈리기 쉽거든요.
두 함수가 서로 같은 함수인지 아닌지 알아보는 방법도 공부할 거예요. 두 함수가 서로 같은지를 확인하는 조건이 있는데, 이 조건을 잘 알아두세요.
정의역, 공역, 치역, 함숫값
함숫값
집합 X에서 집합 Y로의 함수를 f: X → Y라고 나타내죠. 이때 집합 X의 원소에 대응하는 집합 Y의 원소를 함수 f에 의한 x의 함숫값이라고 해요.
기호로는 f: x → y로 나타내기도 하고 y = f(x)로 나타내기도 해요.
X의 임의의 원소 a에 대한 함숫값은 x = a를 대입하면 됩니다. y = f(x)가 y = f(a)가 되는 거예요.
정의역, 공역, 치역
두 집합 X, Y에서 집합 X의 각 원소에 대하여 집합 Y의 원소가 하나씩만 대응할 때, 이 대응을 집합 X에서 집합 Y로의 함수라고 하며, 이것을 기호로 f: X → Y라고 나타내요.
여기서 두 집합 중 X를 함수 f의 정의역, Y를 함수 f의 공역이라고 해요. 또 함숫값 f(x)를 원소로 하는 집합을 함수 f의 치역이라고 해요. 함숫값은 집합 Y의 원소이니까 치역은 공역의 부분집합이죠.
정의역과 공역에 대해서 별다른 언급이 없다면 정의역과 공역은 실수 전체의 집합을 의미합니다.
다음 함수의 정의역, 공역, 치역을 구하여라.
(1) y = x + 1
(2) y = x2 + 1
정의역과 공역에 대한 별다른 얘기가 없으면 실수 전체의 집합으로 생각하세요.
(1) 번의 정의역과 공역은 실수 전체의 집합이에요. 치역은 함숫값들의 집합인데, 정의역이 실수 전체의 집합이니까 x + 1의 결과도 실수 전체의 집합이에요. 따라서 정의역, 공역, 치역이 모두 실수 전체의 집합입니다.
(2) 번도 정의역, 공역에 대한 얘기가 없으니 실수 전체의 집합이에요. x2 + 1에 어떤 값이 들어가더라도 1보다 커요. 따라서 함숫값은 1보다 큰 실수겠죠? 정의역과 공역은 실수 전체의 집합, 치역은{y|y ≥ 1인 실수}네요.
서로 같은 함수
정의역과 공역이 서로 같은 두 함수 f, g가 있어요. f: X → Y, g: U → V
f의 함숫값을 f(x), g의 함숫값을 g(x)라고 할 때, 정의역의 모든 원소 x에 대하여 두 함수의 함숫값이 서로 같으면 f(x) = g(x)가 되죠. 이때 두 함수를 같다고 하고 f = g라고 해요.
두 함수가 서로 같지 않으면 f ≠ g라고 표시합니다.
두 함수 f: X → Y, g: U → V가 같을 조건
정의역과 공역이 같다. X = U, Y = V
모든 원소 x에 대한 함숫값이 같다. f(x) = g(x)
X = {-1, 0, 1}, Y = {0, 1, 4}일 때, 두 함수 f(x) = (x + 1)2, g(x) = (x - 1)2가 서로 같은 함수인지 아닌지를 판별하여라.
두 함수가 같으려면 정의역과 공역이 같고, 함숫값이 같아야 해요. 일단 두 함수의 정의역과 공역이 같네요. 함숫값이 서로 같은지 보죠.
f(-1) = (-1 + 1)2 = 0
f(0) = (0 + 1)2 = 1
f(1) = (1 + 1)2 = 4
g(-1) = (-1 - 1)2 = 4
g(0) = (0 - 1)2 = 1
g(1) = (1 - 1)2 = 0
치역이 같아요. 그래서 언뜻 보면 두 함수는 같은 함수처럼 보여요. 하지만 치역이 같은 건 아무런 상관이 없어요. 함숫값이 같아야 해요. 즉 f(-1) = g(-1), f(0) = g(0), f(1) = g(1)이어야 하죠. 함숫값이 같지 않으니 두 함수 f, g는 서로 같은 함수가 아니에요. f ≠ g
함께 보면 좋은 글
함수, 함수의 정의, 대응
[중등수학/중1 수학] - 함수의 뜻과 함숫값, 함수의 정의
함수, 함수의 정의, 대응
함수는 중학교에서 3년 내내 공부했던 거예요. 함수, 일차함수, 이차함수 그리고 그래프를 공부했었죠? 근데, 기억이 잘 안 나죠? 그래서 이 글에서는 함수의 뜻을 처음부터 다시 정리해볼 거예요.
용어의 의미만 제대로 파악하고 있어도 반은 먹고 들어가는 겁니다. 원소의 의미와 그림을 함께 연결지어서 생각하면 이해하기가 훨씬 쉬울 거예요.
함수는 지난 3년 동안 계속 공부해왔던 것처럼 앞으로 3년 동안 계속 공부할 거니까 이번 기회에 확실히 정리해 놓으세요.
함수
두 집합 X, Y가 있을 때, X의 원소와 Y의 원소를 짝을 지어주는 걸 대응이라고 해요. 대응변, 대응각 들어봤죠? X의 원소 x가 Y의 원소 y와 짝지어질 때, x에 y가 대응한다고 하고 기호로는 x → y라고 나타내요.
두 집합 X, Y에서 집합 X의 각 원소에 대하여 집합 Y의 원소가 하나씩만 대응할 때, 이 대응을 집합 X에서 집합 Y로의 함수라고 하며, 이것을 기호로 f: X → Y라고 나타내요. f는 영어단어 function의 첫 글자 f를 의미합니다.
함수가 되기 위해서는 몇 가지 조건을 만족해야 해요. 첫 번째로 집합 X의 한 원소 x에 집합 Y의 원소 중 하나만 대응해야 해요. 집합 X의 원소에 집합 Y의 원소가 여러 개 대응하면 안 돼요.
두 번째는 집합 X의 모든 원소에 집합 Y의 원소가 대응해야 합니다. 집합 X의 원소 중 집합 Y의 원소와 대응하지 않는 원소가 있으면 안 돼요.
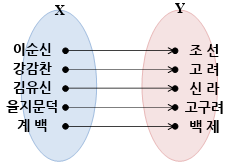
X는 이순신, 강감찬, 김유신, 을지문덕, 계백 원소를 가진 집합이고, Y는 조선, 고려, 신라, 고구려, 백제라는 나라 이름을 원소로 가진 집합이에요.
X에 있는 위인들을 Y에 있는 나라와 연결해봤더니 한 사람에 한 나라씩 대응하죠? 그래서 이 경우는 함수예요.

이번에도 마찬가지로 X에는 사람, Y에는 나라 이름을 연결했어요. 이순신, 김시민, 권율에는 조선이, 온달, 을지문덕에는 고구려가 대응해요. Y에 있는 고려, 신라, 백제에는 대응하는 게 없어요. 하지만 X의 모든 원소에 Y의 원소들이 하나씩 대응하고 있으니까 이 경우도 함수에요.

X의 이성계에 Y의 조선과 고려 두 개가 대응하죠. X의 원소에 Y의 원소가 하나만 대응해야 하는데, 그렇지 않으므로 이 경우는 함수가 아니에요. 이성계는 고려 시대에 살다가 조선을 건국했으니까 양쪽 모두에 대응하도록 연결했어요.

X의 원소들에 Y의 원소들이 하나씩 대응하고 있어요. 그런데 X의 원소 중 단군왕검은 Y의 원소와 대응하고 있지 않죠? X에 대응하지 않은 원소가 있으므로 이 경우도 함수가 아닙니다.
함께 보면 좋은 글
[중등수학/중1 수학] - 함수의 뜻과 함숫값, 함수의 정의
[중등수학/중2 수학] - 일차함수 뜻, 정의역, 공역, 치역
[중등수학/중3 수학] - 이차함수의 뜻, 이차함수란?
부등식의 영역과 최대, 최소
우리가 그리는 좌표평면은 x, y의 값의 한계가 없어요. 끝도 없이 이어지는 영역이라서 최대, 최소를 찾는 게 불가능할 때가 많아요. 이차함수의 최대 최소에서는 최댓값과 최솟값 중 하나만 가지는 경우가 많았어요.
부등식의 영역과 최대, 최소는 일정한 한계가 있는 부등식의 영역 안에서 특정한 값과 식들의 최대, 최소를 구하는 거예요. 한계가 있는 영역이기 때문에 최댓값과 최솟값을 둘 다 구할 수 있어요.
부등식의 영역에서 최댓값과 최솟값을 구하는 방법에 대해서 알아보죠.
부등식의 영역과 최대, 최소
부등식의 영역에서 특정한 값들의 최대, 최소를 구하는 거예요.
x2 + y2 ≤ 4의 영역에서 (x, y)가 움직일 때, x + y의 최댓값과 최솟값을 구해보죠.
x + y = k라고 하면
x + y = k → y = -x + k
y = -x + k에서 k는 이 직선의 방정식의 y절편이므로 y절편의 최댓값과 최솟값을 구하면 돼요.
x2 + y2 ≤ 4의 부등식의 영역과 x + y = k의 그래프를 좌표평면 위에 그려보죠.
y = -x + k는 기울기는 -1로 일정하고 y절편만 바뀌는 직선이니까 m과 n 사이의 직선이에요. m일 때, y절편 즉 k가 최대가 되고, n일 때 k가 최소가 되죠.
k값의 의미는 이해했죠? 그럼 k를 어떻게 구할 거냐? 경계선 x2 + y2 = 4와 직선 y = -x + k가 만나는 점이 있죠? 접점이 있으니까 y = -x + k는 x2 + y2 = 4의 접선의 방정식이에요.
기울기를 알 때 원의 접선의 방정식에서 기울기가 m이고 원에 접하는 방정식은 y = mx ±r이었어요.
이 경우에는 기울기가 -1이고 반지름은 2네요.
y절편이 k이고, k는 x + y이니까 x + y의 최댓값은 , x + y의 최솟값은 -
가 되겠네요.
부등식의 영역에서 최대, 최소를 구하는 방법
- 주어진 부등식의 영역을 좌표평면에 그린다.
- 최대, 최소를 구하는 식 f(x, y) = k로 놓고 이 그래프를 부등식의 영역 안에서 움직여본다.
- k가 최대, 최소일 때의 값을 구한다.
k를 구하는 방법은 여러 가지가 있어요. 하지만 대게 최대, 최소인 값은 접점이나 교점 등에서 생기므로 교점의 좌표를 이용하거나 접점의 성질을 이용하면 k를 구할 수 있어요. 위 경우에서는 접점일 때 최대, 최소가 되었죠?
x ≥ , y ≥ 0인 실수 x, y가 x + y ≤ 1을 만족할 때, x - y의 최댓값 최솟값을 구하여라.
x ≥ , y ≥ 0, x + y ≤ 1의 세 부등식으로 된 부등식의 영역을 좌표평면 위에 그려보죠. 그리고 x - y = k라고 놓으면, y = x - k가 되니까 이 그래프도 그려보고요.
x - y = k의 그래프는 m과 n 사이의 직선으로 교점인 (1, 0)을 지날 때와 (0, 1)을 지날 때 최대, 최소를 가져요.
(1, 0)을 지날 때: x - y = 1 - 0 = 1
(0, 1)을 지날 때: x - y = 0 - 1 = -1
따라서 x - y의 최댓값은 1, 최솟값은 -1입니다.
함께 보면 좋은 글
부등식의 영역 - y > f(x), y < f(x)
부등식의 영역 2 - f(x, y) > 0, f(x, y) < 0
연립부등식의 영역, 연립부등식의 영역 구하기
원의 접선의 방정식 2 - 기울기를 알 때 접선의 방정식
직선의 방정식, 직선의 방정식 구하기
[중등수학/중3 수학] - 이차함수의 최댓값고 최솟값, 이차함수의 최대 최소
연립부등식의 영역, 연립부등식의 영역 구하기
연립부등식의 영역은 부등식의 영역 두 개를 합쳐놓은 걸 말해요. 부등식을 두 개 이상 합쳐놓은 게 연립부등식이니까요.
연립부등식을 푸는 방법과 연립부등식의 영역을 구하는 방법은 근본적으로 같아요. 연립부등식에서는 수직선에 그렸다면 연립부등식의 영역에서는 좌표평면에 그림을 그린다는 차이가 있을 뿐이에요.
그래프를 그려야 해서 복잡해 보이지만 (연립부등식의 영역) = (부등식의 영역) + (연립부등식) 이라는 사실만 기억하고, 관련된 두 내용만 잘 기억하고 있다면 크게 어렵지는 않을 거예요.
연립부등식의 영역
연립부등식의 풀이에서는 각각의 부등식의 해를 구하고 이를 수직선에 그려서 공통인 부분의 해를 찾았어요. 연립부등식의 영역도 똑같아요. 각각의 부등식의 영역을 그린 다음 공통인 부분을 구하면 됩니다.
f(x, y) = 0은 원의 방정식, g(x, y) = 0은 직선의 방정식이라고 한다면, f(x, y) < 0, g(x, y) > 0의 그래프는 아래와 같아요.
f(x, y) < 0, g(x, y) > 0의 공통부분을 칠한 오른쪽 그림이라는 연립부등식의 영역이 됩니다.
식과 부등호의 방향은 바뀌겠지만, 그 방법은 모두 같아요.
연립부등식의 영역
각각의 부등식의 영역을 그린다.
두 부등식의 영역의 공통부분(교집합)을 구한다.
곱으로 표시된 연립부등식의 영역
이번에는 연립부등식이 조금 다른 형태인데요.
f(x, y)·g(x, y) < 0이라는 부등식이에요.
두 식을 곱해서 0보다 작다는 얘기는 부호가 서로 반대라는 얘기예요. 하나가 양수이면 다른 하나는 음수여야 하죠.
총 네 개의 부등식의 영역 그러니까 두 개의 연립부등식의 영역이 생겼어요. or이니까 연립부등식의 영역 두 개를 합한 거예요.
좀 복잡하지만, 집합으로 나타내보면 다음과 같아요.
[{f(x, y) > 0} ∩ {g(x, y) < 0}] ∪ [{f(x, y) > 0} ∩ {g(x, y) < 0}]
이번에는 f(x, y)·g(x, y) > 0을 보죠.
어떤 두 식을 곱해서 0보다 크다는 말은 두 식이 모두 양수이거나 모두 음수여야 하죠?
역시 마찬가지로 네 개의 부등식의 영역, 두 개의 연립부등식이 생겼어요. or이니까 역시 각각의 연립부등식의 영역을 구한 다음 서로 합쳐야 하죠.
부등식의 영역을 네 개가 구해야 하고, 어떤 건 교집합, 어떤 건 합집합이어서 상당히 복잡하죠? 쉽게 구하는 방법이 있어요.
곱으로 표시된 연립부등식의 영역 구하는 순서
- f(x, y) = 0, g(x, y) = 0의 도형의 방정식을 그린다.
- 경계선 위에 있지 않은 임의의 점을 처음 부등식에 대입한다. 계산이 편리한 (0, 0), (1, 0) 등
- 조건에 맞는 영역을 칠한다.
- 대입한 점이 부등식을 만족하면 그 점이 속한 영역 및 건너뛴(이웃하지 않은) 영역
- 대입한 점이 부등식을 만족하지 않으면 그 점이 속하지 않은 영역 및 건너뛴(이웃하지 않은) 영역
다음 부등식의 영역을 좌표평면 위에 나타내어라.
(1)
(2) (x + y - 1)(x2 + y2 - 4) < 0
x2 + y2 < 4의 영역은 왼쪽 그림이고 x + y - 1< 0의 영역은 가운데, 이 둘의 공통부분이 오른쪽 그림이에요.
(2) 번. (x + y - 1)(x2 + y2 - 4) < 0
두 개의 연립부등식의 영역으로 나눠서 구해도 되고, 점을 대입해서 영역을 구해도 돼요. x + y - 1 = 0과 x2 + y2 - 4 = 0의 그래프를 좌표평면에 그렸더니 네 개의 영역으로 나뉘어졌어요.
(0, 0)은 경계선 위에 있지 않으므로 점을 대입해보면
(0 + 0 - 1)(02 + 02 - 4) < 0
4 < 0
부등식을 만족하지 않으므로 (0, 0)이 포함되어 있지 않은 ①번 영역과 ① 영역의 건너뛴(이웃하지 않은) ③ 영역이 구하는 영역이 되겠네요.
함께 보면 좋은 글
부등식의 영역 - y > f(x), y < f(x)
부등식의 영역 2 - f(x, y) > 0, f(x, y) < 0
[중등수학/중2 수학] - 연립부등식, 연립부등식의 풀이
[중등수학/중2 수학] - 여러가지 연립부등식
부등식의 영역 2 - f(x, y) > 0, f(x, y) < 0
앞서 부등식의 영역 - y > f(x), y < f(x)에서는 직선과 이차함수 등 y = f(x) 꼴의 식을 이용하는 부등식의 영역에 대해서 알아봤는데요. 이번에는 f(x, y) = 0 꼴의 식을 이용하는 부등식의 영역에 대해서 알아볼 거예요.
부등식의 모양만 다를 뿐 원리나 그리는 방법 등은 같아요. 특히, 마지막에 나오는 부등식의 영역 그리는 순서는 그래프의 모양과 상관없이 모든 부등식의 영역을 구할 때 사용하는 방법이니까 잘 기억해두세요.
다음에 공부할 연립부등식의 영역을 구하려면 이 글의 내용을 꼭 이해하고 넘어가야 해요.
원의 내부와 외부를 나타내는 부등식
원의 방정식 표준형은 (x - a)2 + (y - b)2 = r2이죠. 좌변은 임의의 점 (x, y)에서 (a, b)까지의 거리를 제곱한 거고 우변은 반지름의 제곱이죠. 즉 원의 방정식은 (a, b)로부터 r만큼의 거리에 있는 점들을 말하는 거예요.
그렇다면 (x - a)2 + (y - b)2 > r2은 무슨 뜻일까요? (a, b)로부터 r보다 더 먼 거리에 있는 점들을 얘기하죠?
그림의 P(x1, y1)에서 원의 중심 C(a, b)까지의 거리는 반지름 r보다 더 커요. 좌표평면 위의 두 점 사이의 거리 공식을 이용해서 식으로 나타내보죠.
즉 원 밖의 임의의 점에서는 (x - a)2 + (y - b)2 > r2이 성립해요. 거꾸로 말해 (x - a)2 + (y - b)2 > r2이 성립하는 점들은 원의 바깥쪽에 있다는 거지요.
같은 방법으로 (x - a)2 + (y - b)2 < r2이 성립하는 점들은 원의 안쪽에 있다는 걸 알 수 있어요.
원의 내부와 외부를 나타내는 부등식
(x - a)2 + (y - b)2 > r2의 영역은 (x - a)2 + (y - b)2 = r2의 바깥쪽
(x - a)2 + (y - b)2 < r2의 영역은 (x - a)2 + (y - b)2 = r2의 안쪽
부등식 f(x, y) > 0, f(x, y) < 0의 영역
도형의 방정식을 f(x, y) = 0으로 나타내잖아요? 그래서 이를 이용한 부등식은 f(x, y) > 0 또는 f(x, y) < 0으로 표시합니다.
이 부등식의 영역을 나타내는 순서는 다음과 같아요.
- 좌표평면에 f(x, y) = 0의 그래프를 그린다.
- 등호가 포함되어 있으면 실선
- 등호가 포함되어있지 않으면 점선
- f(x, y) = 0 위에 있지 않은 임의의 점의 좌표를 대입한다.
- 조건에 맞는 영역을 칠한다.
- 부등식을 만족하면 그 점이 속한 영역
- 부등식을 만족하지 않으면 그 점이 속하지 않은 영역
2단계에서 임의의 점은 (0, 0), (1, 0)처럼 계산을 쉽게 할 수 있는 점들이 좋아요.
다음 부등식의 영역을 좌표평면 위에 나타내어라.
(1) x2 + y2 > 9
(2) (x - 2)2 + (y - 1)2 < 16
일단 f(x, y) = 0의 그래프를 그리고 임의의 점을 대입한 다음 부등식을 만족하면 점이 있는 영역, 부등식을 만족하지 않으면 점이 속하지 않은 영역을 칠하면 돼요.
(1)에 (0, 0)을 대입해보면 0 + 0 > 9로 부등식을 만족하지 않아요. 따라서 (0, 0)이 속하지 않은 영역을 칠해야 해요. 원의 방정식인데, 좌변이 우변인 반지름의 제곱보다 크기 때문에 원의 바깥쪽을 바로 칠해도 되고요.
(2)에 (0, 0)을 대입하면 (-2)2 + (-1)2 < 16으로 부등식을 만족하죠. 따라서 (0, 0)이 속한 영역을 칠하면 되겠네요. 원의 방정식인데, 좌변이 우변인 반지름의 제곱보다 작기 때문에 원의 안쪽을 바로 칠해도 되고요.
함께 보면 좋은 글
부등식의 영역 - y > f(x), y < f(x)
원의 방정식, 원의 방정식 표준형
두 점 사이의 거리, 좌표평면위의 두 점 사이의 거리
부등식의 영역 - y > f(x), y < f(x)
중학교 때, 일차부등식의 풀이에서는 부등식의 해를 수직선 위에 나타냈었잖아요. 부등식의 영역은 부등식을 만족하는 점을 수직선이 아니라 좌표평면에 나타내는 거예요.
설명은 되게 복잡한 것 같지만 식을 그냥 들여다보면 금방 알 수 있을 거예요.
부등식은 등식에서 등호만 부등호로 바뀐 거잖아요. 그래서 부등식의 영역을 그릴 때 등식을 이용해서 그려요. 여기서 이용하는 등식은 이차함수, 직선의 방정식과 원의 방정식 등이에요. 따라서 이들 도형의 방정식을 좌표평면에 나타낼 줄 알아야 해요.
부등식의 영역
x에 대한 일차부등식을 만족하는 x를 수직선에 나타냈던 것처럼 x, y에 대한 부등식을 만족하는 점 (x, y)를 좌표평면에 나타내는데, 이 점 전체의 집합을 부등식의 영역이라고 합니다.
부등식 y > x, y < x의 영역
y = x 그래프와 y축에 평행한 직선, 세 점 P(x, y), Q(x1, y1), R(x2, y2)이 있어요.
점 P(x, y)는 y = x 그래프 위의 점이니까 x좌표와 y좌표가 같아요.
y = x …… ①
점 Q(x1, y1)를 한 번 보죠. y축에 평행한 직선 위에 있으므로 점 P의 x좌표와 점 Q의 x좌표는 같아요.
x = x1 …… ②
점 Q의 y좌표인 y1은 x좌표인 x1보다 크죠?
y1 > x1 …… ③
①, ②, ③에 의해서 y1 > x1 = x = y이므로 y1 > y에요.
y축에 평행한 직선에서 y1 > y가 되는 점 Q는 엄청나게 많겠죠? 점 P보다 위에 있는 점들은 모두 이 조건을 만족하니까요.
y축에 평행한 직선을 왼쪽, 오른쪽으로 움직이면 엄청나게 많은 점 Q를 찾을 수 있고, 이런 점들을 모두 모으면 하나의 영역으로 표시되는데 이게 바로 위 그래프에서 파란색으로 표시된 부분이에요.
이번에는 점 R(x2, y2)를 보죠. y축에 평행한 직선 위에 있으므로 점 R의 x좌표 x2는 점 P의 x좌표와 같아요.
x2 = x …… ④
점 R의 y좌표 y2는 x좌표 x2보다 작고요.
y2 < x2 …… ⑤
①, ④, ⑤에 의해서 y2 < x2 = x = y이므로 y2 < y가 돼요.
마찬가지로 y축에 평행한 직선을 왼쪽, 오른쪽으로 옮기면 엄청나게 많은 점 R을 찾을 수 있고 이 점들을 모두 모으면 하나의 영역으로 표시할 수 있어요.
y > x가 나타내는 영역은 y = x 그래프의 위쪽이고,
y < x가 나타내는 영역은 y = x 그래프의 아래쪽이에요.
부등식 y > f(x), y < f(x)의 영역
y = ax + b의 그래프에요.
같은 방법을 이용하면 y > ax + b를 만족하는 점들의 영역과 y < ax + b를 만족하는 점들의 영역을 찾을 수 있어요.
그래프에서 y = ax + b를 실선이 아닌 점선으로 표시했는데, 이건 y > ax + b, y < ax + b에 등호가 들어있지 않기 때문이에요. 일차부등식의 풀이에서 수직선 위에 부등식을 그릴 때 점을 까맣게 칠하면 ≤, ≥를 나타내고, 하얗게 그리면 <, >를 나타냈던 것과 같아요.
이차함수 그래프 y = ax2 + bx + c와 부등식 y > ax2 + bx + c, y < ax2 + bx + c의 영역을 나타낸 것입니다.
y > f(x)가 나타내는 영역: y = f(x) 그래프의 윗부분
y < f(x)가 나타내는 영역: y = f(x) 그래프의 아랫부분
부등호에 등호가 없으면 y = f(x)는 점선으로 표시
부등식의 영역 그리는 순서
- 기준이 되는 도형의 방정식 y = f(x)의 그래프를 그린다.
이때, 주어진 식의 부등호에 등호가 없으면 점선, 등호가 있으면 실선 - 해당 영역을 색으로 칠한다.
- y > f(x) 또는 y ≥ f(x)이면 그래프보다 위쪽 영역
- y < f(x) 또는 y ≤ f(x)이면 그래프보다 아래쪽 영역
함께 보면 좋은 글
[중등수학/중2 수학] - 일차부등식의 풀이
[중등수학/중2 수학] - 연립부등식, 연립부등식의 풀이
부등식 ax > b의 풀이, 부정, 불능
절댓값 기호를 포함한 일차부등식의 풀이
이차부등식, 이차부등식의 해
이차부등식의 풀이, 판별식과 이차부등식의 해
절대부등식, 부등식의 증명에 이용되는 실수의 성질
대칭이동 - 직선에 대하여 대칭이동(y = x, y = ax + b)
대칭이동 두 번째에요. 점과 도형의 대칭이동에서는 어떤 기준(x축, y축, 원점)을 사용했느냐가 중요하죠. 그리고 그 기준에 따라 대칭이동했을 때 x, y의 좌표가 어떻게 바뀌는지도 알아야 하고요.
이 글에서는 직선 y = x와 y = ax + b에 대하여 대칭이동했을 때 어떻게 바뀌는지 그리고 대칭이동한 결과를 어떻게 구하는지 알아볼 거예요. 직선 y = x에 대한 대칭이동은 앞서 했던 x축, y축, 원점에 대하여 대칭이동과 함께 외워두면 좋고, 직선 y = ax + b에 대하여 대칭이동은 결과를 구하는 과정을 알아두세요.
대칭이동 - 직선에 대하여 대칭이동
y = x에 대하여 대칭이동
좌표평면 위의 한 점을 직선 y = x에 대하여 대칭이동했을 때 어떻게 되는지 알아보죠.
점 P(x, y)를 y = x에 대하여 대칭이동한 점을 점 P'(x', y')라고 해볼까요?
대칭이동하면 직선 y = x에서 점 P까지의 거리와 직선 y = x에서 점 P'까지의 거리가 같아요. 그러니까 점 P와 점 P'에서 같은 거리에 있는 점 바로 선분 PP'의 중점 이 y = x위에 있다는 얘기지요.
또 선분 PP'와 직선 y = x는 서로 수직이에요. 두 직선의 위치관계에서 두 직선이 서로 수직이면 (기울기의 곱) = -1이라고 했어요.
y + y' = x + x' ……… ①
y - y' = -(x - x') ……… ②
이 두 식을 연립해서 풀어보죠.
① + ② : 2y = 2x' → x' = y
① - ② : 2y' = 2x → y' = x
점을 y = x에 대하여 대칭이동하면 x, y의 좌표가 서로 바뀌는 걸 알 수 있어요. P'(x', y') = P'(y, x)가 돼요.
점과 도형의 대칭이동 - x축, y축, 원점에 대하여 대칭이동에서 점의 대칭이동과 도형의 대칭이동은 같다고 했어요. 그러니까 도형의 대칭이동에서도 f(x, y) = 0을 y = x에 대하여 대칭이동하면 f(y, x) = 0이 돼요.
y = x에 대하여 대칭이동
x대신 y대입, y대신 x 대입
점 (x, y)를 y = x에 대하여 대칭이동한 점의 좌표는 (y, x)
도형의 방정식 f(x, y) = 0을 y = x에 대하여 대칭이동한 도형의 방정식은 f(y, x) = 0
다음을 구하여라.
(1) 점 (2, 3)을 y = x에 대하여 대칭이동한 점
(2) 2x + 3y + 4 = 0을 y = x에 대하여 대칭이동한 직선의 방정식
(3) (x - 1)2 + y2 = 10을 y = x에 대하여 대칭이동한 원의 방정식
점과 도형을 y = x에 대하여 대칭이동하면 x → y, y → x로 바꿔주면 돼요.
(1) 번은 (2, 3)이니까 y = x에 대하여 대칭이동하면 (3, 2)가 되겠네요.
(2) 번은 2x + 3y + 4 = 0에서 x와 y를 서로 바꿔주면 2y + 3x + 4 = 0이니까 3x + 2y + 4 = 0이 되겠고요.
(3) 번 (x - 1)2 + y2 = 10에서 x, y를 바꿔주면 (y - 1)2 + x2 = 10이니까 x2 + (y - 1)2 = 10이 되겠네요.
y = ax + b에 대하여 대칭이동
이번에는 점 P(x, y)를 직선 y = ax + b에 대해서 대칭이동해보죠. 대칭이동한 점을 P'(x', y')라고 할게요.
방법은 위와 똑같아요.
- (점 P에서 직선 y = ax + b까지의 거리) = (점 P'에서 직선 y = ax + b까지의 거리)
→ 선분 PP'의 중점이 y = ax + b 위의 한 점 - (선분 PP'의 기울기) × (직선 y = ax + b의 기울기 a) = -1
(x + 1)2 + (y - 2)2 = 10을 y = 2x + 9에 대하여 대칭이동한 도형의 방정식을 구하여라.
원의 방정식을 대칭이동했는데, 원의 방정식 위의 한 점을 대칭이동하는 것도 좋지만, 원의 중심을 이용하는 것도 방법이에요. 대칭이동을 하더라도 반지름의 길이 등 원의 성질은 바뀌지 않으니까요. 원의 중심의 좌표를 대칭이동해보죠.
원의 중심의 좌표를 점 C(-1, 2), 대칭이동한 원의 중심의 좌표를 점 C'(a, b)라고 놓으면
(점 C에서 직선 y = 2x + 9까지의 거리) = (점 C'에서 직선 y = 2x + 9까지의 거리)
→ 선분 CC'의 중점이 y = 2x + 9위의 한 점
중점
(선분 CC'의 기울기) × (직선 y = 2x + 9의 기울기 2) = -1
두 식을 연립해서 풀면 a = -5, b = 4네요. 대칭이동한 원의 방정식의 중심은 (-5, 4)가 되는군요.
(x + 1)2 + (y - 2)2 = 10을 y = 2x + 9에 대하여 대칭이동한 원의 방정식은 (x + 5)2 + (y - 4)2 = 10이 됩니다.
함께 보면 좋은 글
점과 도형의 대칭이동 - x축, y축, 원점에 대하여 대칭이동
평행이동, 점과 도형의 평행이동
두 직선의 위치관계 - 평행, 일치, 수직
선분의 내분점과 외분점
좌표평면 위의 선분의 내분점과 외분점
점과 도형의 대칭이동 - x축, y축, 원점에 대하여 대칭이동
이번에는 점과 도형의 대칭이동입니다. 대칭이동은 그 내용도 쉬운데 이차함수 그래프의 대칭이동에서 해본 적이 있으니까 더 쉬울 거예요. 게다가 평행이동과 달리 점의 좌표의 대칭이동과 도형의 방정식의 대칭이동이 결과가 같으니까 더욱더 쉽죠.
대칭이동에서는 좌표평면에서 항상 함께하는 x축, y축, 원점에 대하여 대칭이동하는 걸 해볼 거고요. 대칭이동했을 때 점의 좌표와 도형의 방정식이 어떻게 바뀌는 지 알아볼 거예요. 대칭이동한 후에 x, y의 좌표가 어떻게 바뀌는지만 주의해서 보면 됩니다.
점과 도형의 대칭이동
대칭이동은 평면 위의 도형을 한 점 또는 한 직선에 대칭인 도형으로 옮기는 걸 말해요. 점에 대하여 대칭이동하는 걸 점대칭, 선에 대하여 대칭이동하는 걸 선대칭이라고 하지요.
점의 좌표의 대칭이동
제 1사분면 위에 (2, 3)라는 점이 있다고 해볼게요. 이 점을 x축, y축, 원점에 대하여 대칭이동 해보죠.
제 1사분면 위의 점 (2, 3)을 x축에 대하여 대칭이동하면 제 4사분면 위의 점 (2, -3)이 되니까 x좌표의 부호 그대로고, y좌표의 부호는 반대로 바뀌어요.
제 1사분면 위의 점 (2, 3)을 y축에 대하여 대칭이동하면 제 2사분면 위의 점 (-2, 3)이 되니까 x좌표의 부호는 반대로 바뀌고, y좌표의 부호는 그대로죠.
제 1사분면 위의 점 (2, 3)을 원점에 대하여 대칭이동하면 제 3사분면 위의 점 (-2, -3)이 되니까 x좌표와 y좌표의 부호가 둘 다 반대로 바뀌어요.
제 1사분면의 점을 예로 들었는데, 제 2사분면의 점도 마찬가지에. 제 2사분면 위의 점 (-2, 3)를 x축에 대하여 대칭이동하면 (-2, 3)가 되니까 x좌표의 부호는 그대로, y좌표의 부호는 반대로 바뀌죠.
이걸 (x, y)라는 점을 이용해서 표현해보죠.
점 (x, y)를 x축에 대하여 대칭이동하면 y → -y
점 (x, y)를 y축에 대하여 대칭이동하면 x → -x
점 (x, y)를 원점에 대하여 대칭이동하면 x → -x, y → -y
주의하세요. x축에 대하여 대칭이동하면 x좌표의 부호가 아니라 y좌표의 부호가 반대로 바뀌고, y축에 대하여 대칭이동하면 y좌표의 부호가 아니라 x좌표의 부호가 반대로 바뀌는 거예요.
원점에 대하여 대한 대칭이동은 x축에 대하여 대칭이동한 점을 다시 y축에 대하여 대칭이동한 것과 같아요. 축과 원점에 대하여 대칭이동하면 값의 절댓값은 그대로고 부호만 바뀌는 것도 알아두세요.
도형의 방정식의 대칭이동
이번에는 도형을 대칭이동해보죠. 도형의 대칭이동은 이차함수 그래프의 대칭이동에서 이미 한 번 해봤던 내용이에요. 그리고 바로 위에서 했던 점의 좌표의 대칭이동과 완전히 같아요.
도형의 방정식을 f(x, y) = 0으로 표현한다고 했어요. f(x, y) = 0을 x축에 대하여 대칭이동한 도형의 방정식을 f(x', y') = 0이라고 해보죠. f(x, y) = 0 위의 임의의 한 점의 좌표를 P(x, y)라고 하고, f(x', y') = 0 위의 한 점을 P'(x', y')라고 하고요.
x' = x → x = x'
y' = -y → y = -y'
도형의 평행이동에서 했던 것과 마찬가지로 원래 알고 있던 식인 f(x, y) = 0에 이 x = x', y = -y'을 대입하면 f(x', -y') = 0이 돼요. 여기서 '을 그냥 떼버리면 f(x, -y) = 0이 되죠.
f(x, y) = 0 → f(x', -y') = 0 → f(x, -y) = 0
y축, 원점에 대하여 대칭이동한 경우도 이런 방법으로 도형의 방정식을 구할 수 있어요.
도형의 방정식 f(x, y) = 0을 x축에 대하여 대칭이동하면 y 대신 -y를 넣으면 돼요. f(x, y) = 0 → f(x, -y) = 0
f(x, y) = 0을 y축에 대하여 대칭이동하면 x 대신 -x를 넣으면 돼요. f(x, y) = 0 → f(-x, y) = 0
f(x, y) = 0을 원점에 대하여 대칭이동하면 x 대신 -x, y 대신 -y를 넣으면 돼요. f(x, y) = 0 → f(-x, -y) = 0
점의 좌표와 도형의 방정식의 대칭이동을 표로 정리해보죠.
| 점의 좌표 | 도형의 방정식 | ||
|---|---|---|---|
| x축 대칭 | y → -y | (x, y) → (x, -y) | f(x, y) = 0 → f(x, -y) = 0 |
| y축 대칭 | x → -x | (x, y) → (-x, y) | f(x, y) = 0 → f(-x, y) = 0 |
| 원점 대칭 | x → -x y → -y |
(x, y) → (-x, -y) | f(x, y) = 0 → f(-x, -y) = 0 |
(x - 4)2 + (y - 2)2 = 10이 나타내는 도형을 x축, y축, 원점에 대하여 대칭이동한 도형의 방정식을 구하여라.
x축에 대하여 대칭이동하면 y → -y로 바꿔줘요.
(x - 4)2 + (y - 2)2 = 10
→ (x - 4)2 + (-y - 2)2 = 10
(x - 4)2 + (y + 2)2 = 10
y축에 대하여 대칭이동하면 x → -x로 바꿔줘요.
(x - 4)2 + (y - 2)2 = 10
→ (-x - 4)2 + (y - 2)2 = 10
(x + 4)2 + (y - 2)2 = 10
원점에 대하여 대칭이동하면 x → -x, y → -y로 바꿔줘요.
(x - 4)2 + (y - 2)2 = 10
→ (-x - 4)2 + (-y - 2)2 = 10
(x + 4)2 + (y + 2)2 = 10
함께 보면 좋은 글
평행이동, 점과 도형의 평행이동
이차함수 그래프의 대칭이동
이차함수 그래프의 평행이동, y = ax2 + q
이차함수 그래프의 평행이동, y = a(x - p)2
이차함수 그래프, y = a(x - p)2 + q
평행이동, 점과 도형의 평행이동
평행이동은 이차함수의 그래프에서 공부했던 거예요. 여기서는 이차함수 그래프의 평행이동을 왜 그렇게 하는지 그 이유를 조금 더 자세히 알아볼 거예요. 그렇다고 대단한 건 아니고 별거 아니에요. 생각보다 쉬워요.
어차피 도형의 평행이동과 이차함수 그래프의 평행이동은 같은 거니까 그 결과만 잘 기억하고 있으면 되는 거죠. 처음 도형과 평행이동한 도형의 관계만 잘 파악하면 돼요.
다만 점의 평행이동과 도형의 평행이동은 작지만 중요한 차이가 있으니 그것만 잘 구별하세요. 점과 도형의 평행이동이 어떻게, 왜 다른지 알아보죠.
점과 도형의 평행이동
좌표평면 위의 점 또는 도형을 일정한 방향으로 일정한 거리 만큼 옮기는 걸 평행이동이라고 해요. 이때 도형의 모양은 바뀌지 않아요. 그 모습 그대로 위치만 바꾸는 겁니다.
점의 평행이동
좌표평면 위의 점 P(x, y)를 평행이동 시켜보죠. x축 방향으로 a만큼, y축 방향으로 b만큼 평행이동한 점의 좌표를 P'(x', y')라고 해볼게요.
x' = x + a
y' = y + b
따라서 점 P'(x', y')의 좌표는 P(x + a, y + b)가 돼요.
a > 0이면 x축에서 오른쪽으로, a < 0이면 x축에서 왼쪽으로 이동하고,
b > 0이면 y축에서 위쪽으로, b < 0이면 y축에서 아래쪽으로 이동해요.
점의 평행이동
점 P(x, y)를 x축 방향으로 a만큼, y축 방향으로 b만큼 평행이동한 점 P'의 좌표는 P'(x + a, y + b)
P(x, y) → P'(x + a, y + b)
도형의 평행이동
도형의 평행이동은 이차함수 그래프, y = a(x - p)2 + q에서 해본 적이 있어요. 이때 y = ax2의 그래프를 x축으로 p만큼, y축으로 q만큼 평행이동하면 y = a(x - p)2 + q가 된다고 했어요. x대신 x - p를 y대신 y - q를 넣는다고 했지요. 이걸 또 하는 거예요.
함수를 y = f(x)라고 하죠? 좌변은 y, 우변은 x에 관한 식이라서 f(x)라고 하는데, 이 둘을 합치니까 y = f(x)가 되는 거예요. 보통 평면좌표 위의 도형의 방정식을 f(x, y) = 0으로 표현해요. 원의 방정식, 직선의 방정식의 일반형의 좌변은 x, y에 관한 식이니까 f(x, y)라고 하고, 우변은 0이잖아요. 이 두 개를 합쳐서 f(x, y) = 0이라고 쓰는 거지요.
어떤 도형이 있다고 해보죠. 그 도형 위의 임의의 점 P(x, y)가 있어요. 이 점 P를 x축으로 a만큼, y축으로 b만큼 평행이동 시킨 점 P'의 좌표를 P'(x', y')라고 해보죠.
x' = x + a → x = x' - a
y' = y + b → y = y' - b
처음의 도형은 x, y에 관한 식이니까 f(x, y) = 0이고, 평행이동한 도형은 x', y'에 대한 식이니까 x', y'라는 문자가 들어간 식으로 표현해야 하잖아요. 그런데 이 새로운 식을 몰라요. 그래서 기존에 알고 있던 식을 변형시켜서 구해야 하는데, 기존에 알고 있던 식이 f(x, y) = 0이죠.
처음 식의 x, y에 x = x' - a, y = y' - b를 대입하면 x, y에 관한 원래 식이 x', y'에 관한 새로운 식으로 바뀌는 거예요. f(x, y) = 0 → f(x' - a, y' - b) = 0
즉, P'(x', y')에 대한 식은 f(x' - a, y' - b) = 0이라는 걸 알 수 있어요.
f(x', y') = 0은 점 P'(x', y')에서 x'와 y'의 관계인데, 가령 점 K(m, n)이라면 f(m – a, n – b) = 0이 될 거고, 점 Z(s, t)라면 f(s – a, t – b) = 0이 될 거예요. 즉 어떤 문자를 사용하든 점의 좌표 중 앞에 있는 문자에서 a를 빼고, 뒤에 있는 문자에서 b를 빼는 식이라는 거죠.
좌표평면에서 도형의 방정식은 x', y'도 아니고 m, n도 아니고 s, t도 아닌 x, y로 나타내죠? 그러니까 x, y의 식 즉 f(x, y)= 0꼴로 나타내야 하니까, 앞에 있는 x에서 a를, 뒤에 있는 y에서 b를 뺀 f(x – a, y – b) = 0이 돼요.
f(x, y) = 0 → f(x' - a, y' - b) = 0 → f(x - a, y - b) = 0
도형의 평행이동
방정식 f(x, y) = 0이 나타내는 도형을 x축 방향으로 a만큼, y축 방향으로 b만큼 평행이동한 도형의 방정식은 f(x - a, y - b) = 0
f(x, y) = 0 → f(x' - a, y' - b) = 0 → f(x - a, y - b) = 0
점의 평행이동에서는 평행이동한 것만큼 더해줬는데, 도형의 평행이동에서는 이동한 만큼 빼주는 거예요. 차이를 잘 기억하세요.
다음을 구하여라.
(1) y = 2x2를 x축으로 3만큼, y축으로 5만큼 이동한 이차함수의 그래프
(2) x2 + y2 - 10 = 0을 x축으로 4만큼, y축으로 -6만큼 이동한 도형의 방정식
도형을 x축으로 a만큼 평행이동하면 x대신 x - a, y축으로 b만큼 평행이동하면 y대신 y - b를 대입해주면 돼요.
(1) 번은 이차함수 그래프의 평행이동이에요.
x축으로 3만큼 평행이동: x → x - 3
y축으로 5만큼 평행이동: y → y - 5
y - 5 = 2(x - 3)2
y = 2(x - 3)2 + 5
(2) 번은 원의 방정식의 일반형이네요.
x축으로 4만큼 평행이동: x → x - 4
y축으로 -6만큼 평행이동: y → y - (-6) = y + 6
(x - 4)2 + (y + 6)2 - 10 = 0
(x - 4)2 + (y + 6)2 = 10
함께 보면 좋은 글
이차함수 그래프의 평행이동, y = ax2 + q
이차함수 그래프의 평행이동, y = a(x - p)2
이차함수 그래프, y = a(x - p)2 + q
원의 접선의 방정식 2 - 기울기를 알 때 접선의 방정식
원의 접선의 방정식 3 - 원 밖의 한 점에서 그은 접선의 방정식
원의 접선의 방정식 세 번째에요. 이번에는 원 밖의 한 점에서 원에 그은 접선의 방정식이에요. 원 안에서는 원에 접선을 그을 수는 없으니까 당연히 원 밖의 한 점이어야겠죠?
여기서는 공식이 나오지 않아요. 게다가 접선의 방정식을 구하는 방법도 기울기를 알 때 접선의 방정식에서 했던 방법을 그대로 사용하니까 이해하기 쉬울 거예요. 대신 계산이 조금 복잡한데 문제에서는 계산하기 쉽게 식을 간단하게 주니까 많이 어렵지는 않을 거예요.
앞에서 충분히 했던 내용이니까 나머지는 그대도 하면 되고, 핵심적인 내용 딱 한 가지만 기억하세요.
원의 접선의 방정식 3 - 원 밖의 한 점에서 그은 접선의 방정식
원 밖의 한 점 P(x1, y1)에서 원 (x - a)2 + (y - b)2 = r2에 그은 접선의 방정식을 구하는 건데 다른 말로는 점 P(x1, y1)을 지나고 원 (x - a)2 + (y - b)2 = r2에 접하는 직선의 방정식이라고도 표현해요. 직선이 2개가 생기죠?
이 직선의 기울기를 아직 모르는데 m이라고 가정해 볼게요. 이게 이 글의 핵심이에요. 기울기를 m으로 놓는 거요. 그럼 우리가 구하려고 하는 접선의 방정식은 기울기가 m이고 점 P(x1, y1)을 지나는 직선이에요. 직선의 방정식 구하기에서 해봤죠?
y - y1 = m(x - x1)
이 직선에서 m을 구하면 식이 완성돼요. m을 구하는 방법은 두 가지에요. 원의 접선의 방정식 2 - 기울기를 알 때 접선의 방정식에서 했던 방법 두 가지와 같아요. 판별식 D를 이용하는 방법과 (원의 중심과 직선 사이의 거리) = (반지름)을 이용하는 방법이요.
위의 직선을 y에 관해서 정리하면 표준형으로 바꿀 수 있어요. y = m(x - x1) + y1
이렇게 y에 관해서 정리한 식을 원의 방정식 (x - a)2 + (y - b)2 = r2에 대입하면 x에 관한 이차방정식이 되고, 여기서 판별식 D = 0일 때, m을 구하면 돼요.
위의 직선을 일반형으로 바꿔보세요. mx - y - mx1 + y1 = 0
원의 중심 (a, b)에서 접선 mx - y - mx1 + y1 = 0까지의 거리가 반지름 r과 같다는 것을 이용해서 m을 구할 수도 있어요.
원 밖의 한 점(x1, y1)에서 원 (x - a)2 + (y - b)2 = r2에 그은 접선의 방정식
기울기를 m이라고 가정하고 y - y1 = m(x - x1)이라는 식을 세운다.
(1) y - y1 = m(x - x1)을 원의 방정식에 대입하여 판별식 D = 0 이용하여 m을 구하거나
(2) 원의 중심(a, b)에서 직선까지의 거리 = 반지름을 이용하여 m을 구한다.
(0, 4)를 지나고 x2 + y2 = 9에 접하는 직선의 방정식을 구하여라.
한 점을 지나고 원에 접하는 직선의 방정식이 바로 한 점에서 그은 접선의 방정식이에요. 같은 말이니까 헷갈리지 마세요.
직선의 방정식의 기울기를 m이라고 가정하면 이 직선이 (0, 4)를 지나니까 식을 세울 수 있어요.
y - 4 = m(x - 0)
y = mx + 4
이 식을 원의 방정식에 대입해보죠.
x2 + (mx + 4)2 = 9
x2 + m2x2 + 8mx + 16 - 9 = 0
(m2 + 1)x2 + 8mx + 7 = 0
D/4 = (4m)2 - (m2 + 1) × 7 = 0
16m2 - 7m2 - 7 = 0
9m2 = 7
m2 =
m = ±
답은 y = ±x + 4
이번에는 판별식이 아니라 원의 중심에서 접선까지의 거리를 이용해서 구해볼까요?
y = mx + 4
mx - y + 4 = 0
원의 중심은 (0, 0)이고 반지름은 3, 접선의 방정식은 mx - y + 4 = 0이에요.
y = ±x + 4로 답이 같죠?
함께 보면 좋은 글
원의 접선의 방정식, 접점을 알 때 접선의 방정식
원의 접선의 방정식 2 - 기울기를 알 때 접선의 방정식
원과 직선의 위치관계
점과 직선사이의 거리 공식, 증명, 유도
직선의 방정식, 직선의 방정식 구하기
직선의 방정식의 일반형, 직선의 방정식의 표준형
원의 접선의 방정식 2 - 기울기를 알 때 접선의 방정식
원의 접선의 방정식 두 번째입니다. 기울기를 알 때에요. 기울기를 알고 있으니까 이미 직선의 방정식의 절반을 알고 있는 거예요. y = mx + n꼴에서 기울기 m을 알고 있으니 y절편 n만 구하면 되겠네요.
원과 직선이 접한다는 건 한 점에서 만난다는 것이고 이는 원과 직선의 위치관계에 했던 내용이에요. 한 점에서 만나는 조건들이 있었는데 이 조건을 이용해서 원의 접선의 방정식을 구할 거예요.
원의 접선의 방정식을 구하는 공식이 나오는데, 외우기 어렵다면 원과 직선의 위치관계를 구하는 과정을 이용해서 문제를 풀어도 좋아요.
원의 접선의 방정식 - 기울기를 알 때
(x - a)2 + (y - b)2 = r2에 접하고 기울기가 m인 접선을 구해보죠.
원과 직선의 위치관계에서 원과 직선이 한 점에서 만날 때 판별식 D = 0이거나 (원의 중심에서 접선까지의 거리) = (반지름)인 관계가 있다고 했어요. 이를 이용해서 접선의 방정식을 구해요.
위 그림에 보면 접선의 방정식이 2개가 그려져 있어요. 기울기는 같고 y절편만 다른 두 개의 접선의 방정식이 생기기 때문이에요. 이 두 개를 모두 구해야 합니다.
판별식 D를 이용
먼저 x2 + y2 = r2에 접하는 접선의 방정식을 구해보죠. 접선의 방정식을 y = mx + k라고 하고 이 방정식을 원의 방정식에 대입해서 정리해서 D를 구해볼까요?
x2 + y2 = r2
x2 + (mx + k)2 = r2
x2 + m2x2 + 2mkx + k2 = r2
(m2 + 1)x2 + 2mkx + k2 - r2 = 0
D/4 = m2k2 - (m2 + 1)(k2 - r2) = 0
m2k2 - m2k2 + m2r2 - k2 + r2 = 0
m2r2 - k2 + r2 = 0
k2 = m2r2 + r2
k2 = r2(m2 + 1)
k = ±r
x2 + y2 = r2에 접하는 접선의 방정식은 y = mx ±r이에요.
이차함수 그래프, y = (x - p)2 + q는 y = x2의 그래프를 x축으로 p만큼 이동해서 x 대신 x - p를, y축으로 q만큼 이동해서 y 대신 y - q를 넣어 준거라고 했어요. 꼭짓점이 (0, 0)에서 (p, q)로 이동했잖아요. 원의 방정식 (x - a)2 + (y - b)2 = r2은 x2 + y2 = r2을 x축으로 a만큼, y축으로 b만큼 이동한 원의 방정식이에요. 원의 중심이 (0, 0)에서 (a, b)로 이동했어요. 그래서 접선의 방정식도 x 대신 x - a, y대신 y - b를 넣어주면 돼요.
(x - a)2 + (y - b)2 = r2의 제곱에 접하고 기울기가 m인 접선의 방정식은 y = mx ± r에 x 대신 x - a, y 대신 y - b를 넣어준 y - b = m(x - a) ± r
이 됩니다.
원의 중심과 접선까지의 거리 이용
x2 + y2 = r2의 중심에서 y = mx + k까지의 거리는 반지름 r과 같아요.
원의 중심 (0, 0)
y = mx + k → mx - y + k = 0
점과 직선 사이의 거리 공식에 대입해보죠.
따라서 y = mx ± r이죠.
위와 같은 이유로 x축으로 a만큼 이동하며 x 대신 x - a를, y축으로 b만큼 이동하면 y 대신 y - b를 대입해요.
x2 + y2 = r2의 접선의 방정식은 y = mx ± r
(x - a)2 + (y - b)2 = r2의 접선의 방정식 y - b = m(x - a) ± r
기울기가 m인 원의 접선의 방정식
판별식 D를 이용: 접선의 방정식 표준형을 원의 방정식에 대입하고 D = 0이 되는 값을 구한다.
원의 중심에서 접선의 방정식까지의 거리 이용: (원의 중심에서 접선의 방정식까지의 거리) = (반지름 r) 이용
x2 + y2 = r2에 접하고 기울기가 m인 접선의 방정식: y = mx ± r
(x - a)2 + (y - b)2 = r2에 접하고 기울기가 m인 접선의 방정식: y - b = m(x - a) ± r
공식에서 (y - b)와 (x - a)는 원의 방정식에 있는 걸 그대로 가져다 쓰면 되니까 더 쉽죠?
다음을 구하여라.
(1) x2 + y2 = 16에 접하고 y = x - 1에 평행한 접선의 방정식
(2) (x - 1)2 + (y + 2)2 = 25에 접하고 기울기가 3인 접선의 방정식
(1) y = x - 1에 평행한 그래프니까 두 직선의 위치관계에 따라 기울기가 1이네요. y = x + k라고 해보죠.
x2 + (x + k)2 = 16
x2 + x2 + 2kx + k2 - 16 = 0
2x2 + 2kx + k2 - 16 = 0
D/4 = k2 - 2(k2 - 16) = 0
k2 - 2k2 + 32 = 0
k2 = 32
k = ±
k = ±4
따라서 접선의 방정식은 y = x ± 4
(2)번은 공식에 대입해서 구해볼까요?
y - b = m(x - a) ± r
y + 2 = 3(x - 1) ± 5
y = 3x - 5 ± 5
함께 보면 좋은 글
원의 접선의 방정식, 접점을 알 때 접선의 방정식
원과 직선의 위치관계
점과 직선사이의 거리 공식, 증명, 유도
두 직선의 위치관계 - 평행, 일치, 수직
두 원의 교점을 지나는 원의 방정식
축에 접하는 원의 방정식
세 점을 지나는 원의 방정식, 원의 방정식 일반형
원의 방정식, 원의 방정식 표준형
원의 접선의 방정식, 접점을 알 때 접선의 방정식
원 위의 한 점을 지나는 직선의 방정식을 구할 거예요. 원과 직선이 만나는 한 점을 접점이라고 하고, 접점을 지나는 직선의 방정식이니까 원의 접선의 방정식이라고 해요.
접선의 방정식도 직선의 방정식의 한 종류니까 직선의 방정식 구하기를 이용하여 구합니다. 또 접선의 방정식은 원 위의 한 점을 지나니까 이를 이용하기도 하고요.
접선의 방정식을 구하는 경우는 여러 가지가 있지만, 이 글에서는 접점의 좌표를 알 때 접선의 방정식 구하는 방법을 알아볼 거예요.
원의 접선의 방정식, 접점을 알 때 접선의 방정식
원의 방정식 (x - a)2 + (y - b)2 = r2위의 한 점에서 접하는 접선의 방정식 l을 구해보죠. 원의 중심을 C(a, b), 접점의 좌표를 P(x1, y1)라고 할게요.
원의 접선은 반지름에 수직이에요. 선분 CP가 반지름이므로 구하고자 하는 접선의 방정식 l과 수직이죠. 두 직선의 위치관계에서 두 직선이 수직이면 (기울기의 곱) = -1이라고 했죠? 직선 l의 기울기를 m이라고 해보죠.
직선 l은 기울기가 m이고, P(x1, y1)을 지나는 직선이니까 직선의 방정식 구하는 공식에 넣어보면 ……… ①
일반적으로 기울기는 인데, 원의 접선의 방정식 l은 기울기는 거꾸로예요. 그리고 앞에 (-)가 붙고요.
①의 공식으로 접선의 방정식을 구할 수도 있지만 다른 공식이 또 있어요.
접점 P(x1, y1)는 원의 방정식 (x - a)2 + (y - b)2 = r2위의 접이기도 해요. (x1, y1)을 대입해보죠.
(x1 - a)2 + (y1 - b)2 = r2 ……… ②
①, ②식을 각각 전개해서 더한 다음에 인수분해하면 아래 공식을 유도할 수 있어요. 유도 과정은 길어서 생략할게요.
(x1 - a)(x - a) + (y1 - b)(y - b) = r2
원래 원의 방정식은 (x - a)(x - a) + (y - b)(y - b) = r2인데, (x1 - a)(x - a) + (y1 - b)(y - b) = r2으로 바뀌었죠? x 하나가 x1으로, y 하나가 y1으로 바뀐 형태예요……
원의 접선의 방정식
(x - a)2 + (y - b)2 = r2위의 접점 P(x1, y1)을 지나는 접선의 방정식
(x1 - a)(x - a) + (y1 - b)(y - b) = r2
두 가지다 같은 결과가 나옵니다. 보통은 원의 방정식의 모양과 비슷해서 외우기 쉬운 두 번째를 많이 사용하는데, 본인이 외우기 쉬운 공식을 외우세요.
다음을 구하여라.
(1) (x - 2)2 + (y + 1)2 = 5 위의 점 (3, -3)에서의 접선의 방정식
(2) (x + 3)2 + (y + 1)2 = 50 위의 점 (4, -2)에서의 접선의 방정식
(3) x2 + y2 + 6x - 2y - 7 = 0위의 점 (-2, -3)에서의 접선의 방정식
(1) 번은 원의 중심이 (2, -1)이고 접점의 좌표는 (3, -3), r2 = 5예요.
(x1 - a)(x - a) + (y1 - b)(y - b) = r2
(3 - 2)(x - 2) + (-3 + 1)(y + 1) = 5
x - 2 - 2y - 2 - 5 = 0
x - 2y - 9 = 0
어떤 공식을 이용하든 결과가 똑같죠?
(2) 원의 중심은 (-3, -1), 접점의 좌표는 (4, -2), r2 = 50이네요.
(x1 - a)(x - a) + (y1 - b)(y - b) = r2
(4 + 3)(x + 3) + (-2 + 1)(y + 1) = 50
7x + 21 - y - 1 = 50
7x - y - 30 = 0
(3) 번은 먼저 표준형으로 바꿔야겠네요.
x2 + y2 + 6x - 2y - 7 = 0
x2 + 6x + y2 - 2y - 7 = 0
(x + 3)2 + (y - 1)2 - 7 - 9 - 1 = 0
(x + 3)2 + (y - 1)2 = 17
원의 중심이 (-3, 1)이고 접점의 좌표가 (-2, -3), r2 = 17이군요.
(x1 - a)(x - a) + (y1 - b)(y - b) = r2
(-2 + 3)(x + 3) + (-3 - 1)(y - 1) = 17
x + 3 - 4y + 4 = 17
x - 4y - 10 = 0
함께 보면 좋은 글
원의 접선의 방정식 2 - 기울기를 알 때
원의 접선의 방정식 3 - 원 밖의 한 점에서 그은 접선의 방정식
원의 방정식, 원의 방정식 표준형
두 원의 교점을 지나는 원의 방정식
원과 직선의 위치관계
원과 직선의 위치관계
기억나진 않겠지만, 원과 직선의 위치관계는 중학교 1학년 때 원과 직선의 위치관계에서 공부했었어요. 이때는 그림을 보면서 어떤 위치관계가 있는지만을 공부했었죠.
이제는 단순히 원과 직선의 위치관계의 종류뿐 아니라 그러한 위치를 갖는 조건을 알아볼 거예요. 물론 위치관계를 가질 조건은 원의 방정식과 직선의 방정식의 관계를 말하죠. 주어진 식을 이용해서 원과 직선에 어떤 관계가 있을 때, 어떤 위치관계에 있는지를 알아보죠.
앞서 했던 여러 단원의 내용이 광범위하게 나오니까 전에 공부했던 내용을 잘 떠올려보세요.
원과 직선의 위치관계
원과 직선의 위치관계는 그림에서 보듯이 서로 다른 두 점에서 만날 때, 한 점에서 만날 때, 만나지 않을 때 세 가지 경우가 있어요. 한 점에서 만날 때를 접한다고 하고요.

판별식 이용
원의 방정식은 x, y에 관한 이차방정식이고 직선의 방정식은 x, y에 관한 일차방정식이에요. 그래프에서의 교점은 원의 방정식의 해이면서 직선의 방정식의 해 즉 연립방정식의 해고요. 그러니까 교점의 개수를 구하는 건 연립방정식의 해의 개수를 구하는 것과 같아요.
이차방정식과 일차방정식으로 된 연립방정식은 일차식을 한 문자에 관해서 정리한 후에 이차식에 대입해서 풀었어요. 여기서도 이 방법을 이용합니다.
일차식인 직선의 방정식을 한 문자에 관해서 정리한 후에 이차식인 원의 방정식에 대입하면 그 식은 이차식이에요. 이 이차식의 해의 개수가 연립방정식의 해의 개수이고, 이건 이차방정식의 판별식을 이용해서 구할 수 있어요.
- 일차식인 직선의 방정식을 한 문자에 관해서 정리
- 1의 식을 이차식인 원의 방정식에 대입. 전개
- 2의 식에서 판별식 D를 구한다.
D > 0 ⇔ 서로 다른 두 실근 ⇔ 서로 두 점에서 만난다.
D = 0 ⇔ 중근 ⇔ 한 점에서 만난다. (접한다.)
D < 0 ⇔ 허근 ⇔ 만나지 않는다.
직선을 y에 대해서 정리한 형태가 바로 직선의 방정식의 표준형이에요. 그리고 이걸 원의 방정식에 대입하여 판별식을 구하는 이차식은 일반형이고요.
원의 중심에서 직선까지의 거리 이용
점과 직선 사이의 거리 공식을 이용할 수도 있어요. 원의 방정식에서 원의 중심의 좌표를 구한 다음 원의 중심과 직선 사이의 거리를 구하고 이를 원의 반지름과 비교하는 거예요.
원의 중심과 직선 사이의 거리를 d, 원의 반지름을 r이라고 해보죠.
d < r ⇔ 서로 다른 두 점에서 만난다.
d = r ⇔ 한 점에서 만난다. (접한다.)
d > r ⇔ 만나지 않는다.
원의 중심을 구하려면 원이 표준형으로 되어 있어야겠죠? 원과 직선 사이의 거리를 구할 때 직선의 방정식은 일반형이고요.
위의 내용을 표로 정리해보죠.
| 판별식 D 이용 | 원의 중심과 직선 사이의 거리 이용 | |
|---|---|---|
| 형태 | 원의 방정식: 일반형 직선의 방정식: 표준형 |
원의 방정식: 표준형 직선의 방정식: 일반형 |
| 방법 | 직선의 방정식을 한 문자에 관하여 정리한 후 원의 방정식에 대입하여 판별식 이용 | 원의 중심과 직선의 방정식 사이의 거리 이용 |
| 서로 다른 두 점 | D > 0 | d < r |
| 한 점 | D = 0 | d = r |
| 만나지 않는다. | D < 0 | d > r |
다음 원의 방정식과 직선의 방정식이 서로 다른 두 점에서 만나기 위한 k의 조건을 구하여라.
(1) x2 + y2 + 4x + 8y + k - 8 = 0, x + y - 4 = 0
(2) (x - k)2 + (y + 2)2 = 5, x + 2y + 10 = 0
(1)번은 원의 방정식은 일반형, 직선의 방정식도 일반형이네요. 원의 방정식은 일반형이라면 직선의 방정식이 표준형이어야 판별식을 이용할 텐데 말이죠. 그런데 이때는 직선의 방정식을 그냥 표준형으로 바꾸면 돼요. 표준형으로 바꾸는 건 정말 쉬우니까요.
x + y - 4 = 0
y = -x + 4
이 식을 원의 방정식에 대입해보죠.
x2 + (-x + 4)2 + 4x + 8(-x + 4) + k - 8 = 0
x2 + x2 - 8x + 16 + 4x - 8x + 32 + k - 8 = 0
2x2 - 12x + k + 40 = 0
이차식이 만들어졌는데, 이차식의 해의 개수가 두 방정식의 교점의 개수와 같아요. 서로 다른 두 실근을 가진다고 했으니 D > 0이어야겠네요.
D/4 = 62 - 2(k + 40) > 0
36 - 2k - 80 > 0
2k < -44
k < -22
(2) 원의 방정식은 표준형, 직선의 방정식은 일반형이에요. 이때는 원의 중심과 직선 사이의 거리를 이용해요.
원의 중심의 좌표는 (k, -2), 반지름은 예요.
절댓값 기호를 풀 때는 절댓값 기호를 포함한 일차부등식의 풀이를 이용했어요.
함께 보면 좋은 글
원의 방정식, 원의 방정식 표준형
점과 직선 사이의 거리 공식, 증명, 유도
직선의 방정식의 일반형, 직선의 방정식의 표준형
연립방정식 - 연립이차방정식의 풀이
절댓값 기호를 포함한 일차부등식의 풀이
두 원의 교점을 지나는 원의 방정식
두 원의 교점을 지나는 원의 방정식은 두 직선의 교점을 지나는 직선의 방정식과 거의 비슷해요. 두 직선의 교점을 지나는 직선의 방정식에서 표준형이 아니라 일반형을 이용했어요. 그리고 항등식의 성질을 이용했죠. 두 원의 교점을 지나는 원의 방정식에서도 일반형과 항등식의 성질을 이용합니다.
차이가 있다면 때에 따라서는 원의 방정식이 아니라 두 원의 교점을 지나는 직선의 방정식이 나올 수도 있다는 거예요. 어떤 경우에 원의 방정식이 되고, 어떤 경우에 직선의 방정식이 되는지 잘 알아두세요.
두 원의 교점을 지나는 원의 방정식
그림에서 보듯이 두 원의 교점을 지나는 원의 방정식은 무수히 많아요. 그래서 교점만 가지고는 원의 방정식을 구할 수 없죠. 대게 문제에서는 교점이 아닌 다른 점의 좌표를 주거나 다른 힌트를 줍니다. 다른 힌트를 대입할 수 있게 미리 원의 방정식을 만들어야 해요.
두 직선의 교점을 지나는 직선의 방정식에서 ax + by + c = 0과 a'x + b'y + c' = 0의 교점을 지나는 직선의 방정식은 ax + by + c + k(a'x + b'y + c') = 0이라고 했어요. (직선의 방정식 1) + k(직선의 방정식 2) = 0이었죠.
두 원의 교점을 지나는 원의 방정식도 똑같아요. 두 원의 방정식을 x2 + y2 + Ax + By + C = 0, x2 + y2 + A'x + B'y + C' =0이라고 한다면 (원의 방정식 1) + k(원의 방정식 2) = 0으로 두면 돼요.
이 방정식도 k에 관한 항등식을 이용해서 증명할 수 있어요.
두 원 x2 + y2 + Ax + By + C = 0과 x2 + y2 + A'x + B'y + C' = 0의 교점을 지나는 원의 방정식
⇔ (원의 방정식 1) + k(원의 방정식 2) = 0
⇔ x2 + y2 + Ax + By + C + k(x2 + y2 + A'x + B'y + C') = 0
두 원의 교점을 지나는 직선의 방정식
그런데 k = -1일 때를 보죠.
x2 + y2 + Ax + By + C - (x2 + y2 + A'x + B'y + C') = 0
x2 + y2 + Ax + By + C - x2 - y2 - A'x - B'y - C') = 0
(A - A')x + (B - B')y + (C - C') = 0
전개한 결과는 ax + by + c = 0꼴의 직선의 방정식의 일반형이에요. 즉 k = -1일 때는 두 원의 교점을 지나는 원의 방정식이 아니라 두 원의 교점을 지나는 직선의 방정식이 된다는 걸 알 수 있어요.
두 원의 방정식이 x2 + y2 - 2x + 14y - 50 = 0과 x2 + y2 + 6x + 8y - 25 = 0일 때, 다음 물음에 답하여라.
(1) 두 원의 교점과 (0, 0)을 지나는 원의 방정식
(2) 두 원의 교점을 지나는 직선의 방정식
두 원의 교점을 지나는 원의 방정식은 x2 + y 2 + Ax + By + C + k(x2 + y2 + A'x + B'y + C') = 0이에요. k ≠ -1이면 원의 방정식이고, k = -1이면 직선의 방정식이 되죠.
(1)번은 x2 + y2 - 2x + 14y - 50 + k(x2 + y2 + 6x + 8y - 25) = 0인데, 이 원의 방정식이 원점 (0, 0)을 지나니까 (0, 0)을 대입해보죠.
-50 + k(-25) = 025k = -50
k = -2
k = -2를 원래의 식에 대입하면
x2 + y2 - 2x + 14y - 50 - 2(x2 + y2 + 6x + 8y - 25) = 0
x2 + y2 - 2x + 14y - 50 - 2x2 - 2y2 -12x -16y + 50 = 0
-x2 - y2 - 14x - 2y = 0
x2 + y2 + 14x + 2y = 0
(2)번은 x2 + y2 - 2x + 14y - 50 + k(x2 + y2 + 6x + 8y - 25) = 0에서 k = -1이면 돼요.
x2 + y2 - 2x + 14y - 50 - (x2 + y2 + 6x + 8y - 25) = 0
x2 + y2 - 2x + 14y - 50 - x2 - y2 - 6x - 8y + 25 = 0
-8x + 6y - 25 = 0
8x - 6y + 25 = 0
함께 보면 좋은 글
원의 방정식, 원의 방정식 표준형
세 점을 지나는 원의 방정식, 원의 방정식 일반형
아폴로니오스의 원, 아폴로니오스의 원 증명
축에 접하는 원의 방정식
두 직선의 교점을 지나는 직선의 방정식
직선의 방정식의 일반형, 직선의 방정식의 표준형
항등식과 항등식의 성질
축에 접하는 원의 방정식
직선의 방정식에서는 축과 만나는 점이 있었어요. 그걸 x, y절편이라고 부르죠. x, y절편의 좌표를 이용해서 직선의 방정식을 구할 수 있었어요.
원의 방정식에서는 축과 단순히 만나는 게 아니라 접하는 경우에 대해서 공부할 거예요. x, y축에 접하는 원의 방정식은 어떤 특징이 있는지 알아보고, 이를 이용해서 축에 접하는 원의 방정식을 구하는 방법도 알아볼 거예요.
그냥 식만 생각하기보다는 그래프를 종이에 그려보면 조금 더 쉽게 문제를 풀 수 있어요. 특징이 간단하니까 그래프만 그리면 문제는 금방 풀 수 있어요.
축에 접하는 원의 방정식
x축에 접하는 원의 방정식
위 그림에서 원의 중심의 좌표는 (a, b)에요. 그런데 원이 x축에 접하고 있으므로 중심의 y좌표는 반지름 r과 같아요. b = r
원이 제 1사분면이 아니라 제 4사분면에 있다면 어떨까요? 그때도 b = r이 될까요? 원이 제 4사분면에 있다면 b < 0이에요. 반지름 r은 길이니까 무조건 0보다 커야 해요. 이때는 -b = r이라고 해야겠죠?
두 경우에 모두 적용될 수 있게 |b| = r이라고 합니다.
원이 제 1사분면에 있든 제 4사분면에 있든 상관없이 b2 = r2이니까 (x - a)2 + (y - b)2 = r2을 (x - a)2 + (y - b)2 = b2이라고 쓸 수 있어요.
x축에 접하는 원의 방정식
반지름 = 중심의 y좌표의 절댓값
r = |b|
(x - a)2 + (y - b)2 = b2
y축에 접하는 원의 방정식
위 그림에서 원의 중심의 좌표는 (a, b)에요. 그런데 원이 y축에 접하고 있으므로 중심의 x좌표는 반지름 r과 같아요. a = r
원이 제 1사분면이 아니라 제 2사분면에 있다면 어떨까요? 그때도 a = r이 될까요? 원이 제 2사분면에 있다면 a < 0이에요. 반지름 r은 길이니까 무조건 0보다 커야 해요. 따라서 두 경우에 모두 적용될 수 있게 |a| = r이라고 해야겠죠?
여기서도 원이 위치한 사분면에 관계없이 a2 = r2니까 (x - a)2 + (y - b)2 = a2이라고 쓸 수 있어요.
y축에 접하는 원의 방정식
반지름 = 중심의 x좌표의 절댓값
r = |a|
(x - a)2 + (y - b)2 = a2
x, y축에 접하는 원의 방정식
위 그림에서 원의 중심의 좌표는 (a, b)에요. 그런데 원이 x, y축에 접하고 있으므로 중심의 x좌표와 중심의 y좌표, 반지름 r이 같아요. a = b = r
그런데, a, b는 원이 위치한 사분면에 따라서 부호가 달라져요. a또는 b가 (-)가 될 수 있다는 얘기지요. r은 양수여야 하니까 |a| = |b| = r이라고 해야 합니다.
앞선 두 경우에는 r을 a 또는 b로 대신 썼는데, 이번에는 반대로 a, b를 r로 바꿔서 나타내보죠.
원이 제 1사분면에 있으면 원의 중심은 둘 다 (+)니까 원의 중심을 (r, r)이고 할 수 있죠.
(x - r)2 + (y - r)2 = r2
원이 제 2사분면에 있으면 원의 중심의 x좌표는 (-), y좌표는 (+)에요. 원의 중심을 (-r, r)이고 할 수 있어요.
(x + r)2 + (y - r)2 = r2
원이 제 3사분면에 있으면 원의 중심은 둘 다 (-)니까 원의 중심을 (-r, -r)이고 할 수 있어요.
(x + r)2 + (y + r)2 = r2
원이 제 4사분면에 있으면 원의 중심의 x좌표는 (+), y좌표는 (-)에요. 원의 중심을 (r, -r)이고 할 수 있어요.
(x - r)2 + (y + r)2 = r2
| 원의 위치 | 중심의 좌표 | 원의 방정식 |
|---|---|---|
| 제 1사분면 | (r, r) | (x - r)2 + (y - r)2 = r2 |
| 제 2사분면 | (-r, r) | (x + r)2 + (y - r)2 = r2 |
| 제 3사분면 | (-r, -r) | (x + r)2 + (y + r)2 = r2 |
| 제 4사분면 | (r, -r) | (x - r)2 + (y + r)2 = r2 |
x, y축에 접하는 원의 방정식
반지름 = 중심의 x좌표의 절댓값 = 중심의 y좌표의 절댓값
r = |a| = |b|
다음 원의 방정식을 구하여라.
(1) 중심의 좌표가 (1, 2)이고 x축에 접하는 원의 방정식
(2) 중심의 좌표가 (-3, -4)이고, y축에 접하는 원의 방정식
(3) 반지름의 길이가 5이고 제 4사분면에서 x, y축에 접하는 원의 방정식
중심이 (a, b)이고 반지름이 r인 원의 방정식은 (x - a)2 + (y - b)2 = r2이에요.
x축에 접하는 원이라면 중심의 y좌표의 절댓값과 반지름이 같고, y축에 접하는 원이라면 중심의 x좌표의 절댓값과 반지름이 같아요. x, y축에 동시에 접하는 원이라면 (중심의 x좌표 절댓값)= (중심의 y좌표 절댓값) = (반지름 r)이고요.
(1)은 x축에 접하는 원의 방정식이니까 |중심의 y좌표| = |2| = r
(x - 1)2 + (y - 2)2 = 22
(x - 1)2 + (y - 2)2 = 4
(2)는 y축에 접하는 원의 방정식이니까 |중심의 x좌표| = |-3| = r
(x + 3)2 + (y + 4)2 = 32
(x + 3)2 + (y + 4)2 = 9
(3)은 x, y축에 접하는 원의 방정식이니까 |중심의 x좌표| = |중심의 y좌표| = r이에요. 그런데, 제 4사분면 위에 있으니까 중심의 x좌표는 (+), 중심의 y좌표는 (-)에요. 원의 반지름이 5니까 중심의 좌표는 (5, -5)네요.
(x - 5)2 + (y + 5) 2= 52
(x - 5)2 + (y + 5)2 = 25
함께 보면 좋은 글
원의 방정식, 원의 방정식 표준형
세 점을 지나는 원의 방정식, 원의 방정식 일반형
아폴로니오스의 원, 아폴로니오스의 원 증명










































