이제는 함수의 정의에 이어 함수의 종류에 대해서 공부할 거예요. 함수의 종류에는 여러 가지가 있는데, 그중에서 일대일함수, 일대일 대응, 항등함수, 상수함수에 대해서만 알아보죠. 특히, 일대일함수와 일대일 대응은 헷갈리기 쉬우니까 그 차이를 분명히 알아두세요.
또, 항등함수와 상수함수는 그 의미만 간단히 이해하고 있으면 되는 비교적 쉬운 함수입니다.
일대일함수와 일대일 대응
함수는 집합 X의 원소 x 한 개에 집합 Y의 원소 y 한 개가 대응하는 관계를 말해요. 거꾸로 y 한 개가 x 여러 개에 대응해도 함수는 함수에요. 아래 그림처럼 연결돼도 함수라고 할 수 있는 거죠.
X의 이순신, 김시민, 권율이 Y의 조선에 대응해요. 거꾸로 보면 Y의 조선은 X의 이순신, 김시민, 권율 세 명과 대응하죠.
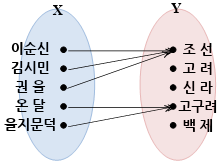
위 그림과 달리 함수 중에서 y 한 개가 여러 개의 x에 대응하지 않는 경우를 일대일함수라고 해요. x 한 개에 y 한 개가 대응하고, y 한 개가 x 한 개에 대응하는 관계요. 아래 함수에서 Y의 원소들은 X의 원소 한 개와만 대응해요.
이걸 식으로 표현하면 x1 ∈ X, x2 ∈ X이고, x1 ≠ x2일 때, f(x1) ≠ f(x2)라고 표현할 수 있어요. x가 다르면 그에 대응하는 y도 다르다는 얘기예요.
일대일함수 중에서 공역과 치역이 같은 함수를 일대일 대응이라고 해요. 일대일 대응은 일대일함수의 조건을 만족한 상태에서 추가로 공역과 치역이 같아야 하니까 일대일 대응은 일대일함수의 부분집합이라고 생각하면 쉬워요.
일대일함수:집합 X의 임의의 원소 x1, x2에 대하여 x1 ≠ x2일 때, f(x1) ≠ f(x2)인 함수
일대일 대응: 일대일함수 + (공역 = 치역)
다음 그림을 보고, 일대일함수와 일대일 대응을 구분하여라.
집합 X의 원소 x1에 대하여 f(x1) ∈ Y이면 함수에요.
여기에서 x1 ≠ x2일 때, f(x1) ≠ f(x2)이면 일대일함수고요.
또 공역 = 치역이면 일대일 대응이에요.
조건을 만족하는 개수에 따라 함수 → 일대일함수 → 일대일 대응의 순서가 되는 거죠.
왼쪽 그림은 집합 X의 원소 다섯 개에 Y의 원소 한 개가 대응하니까 함수에요. f(1) = f(2)니까 그냥 함수에요.
가운데 그림은 집합 X의 원소에 대응하는 집합 Y의 원소가 다 달라요. 그런데 공역은 {a, b, c, d, e}이고 치역은 {a, b, c, d}로 공역 ≠ 치역이라서 일대일함수네요.
오른쪽 그림은 집합 X의 원소에 대응하는 집합 Y의 원소가 다 다르므로 일대일함수인데, 여기에 치역 = 공역이니까 일대일 대응이네요.
항등함수와 상수함수
항등식 알죠? 항등식은 항상 성립하는 등식이에요. 여기서 항등은 항상 같다는 뜻이죠. 항등함수에서 항등도 같은 뜻이에요. 집합 X의 원소와 이에 대응하는 집합 Y의 원소가 항상 같다는 얘기죠.
집합 X의 임의의 원소 x에 대하여 f(x) = x인 함수를 말해요.
집합 X의 원소 1에는 집합 Y의 원소 1이 대응해요. 2에는 2가 대응하고요. 항상 자기 자신과 같은 값이 대응하죠?
위 그림에서 X의 1, 2, 3, 4, 5가 모두 Y의 c에만 대응해요. 이처럼 X의 모든 원소가 Y의 한 원소와만 대응하는 경우를 상수함수라고 해요.
항등함수: 집합 X의 임의의 원소 x에 대하여 f(x) = x인 함수
상수함수: 집합 X의 임의의 원소 x에 대하여 f(x) = c인 함수
함께 보면 좋은 글
함수, 함수의 정의, 대응
정의역, 공역, 치역, 함숫값, 서로 같은 함수
함수의 그래프